We often hear such verbal designs, as "Machine training", "Neural networks". These expressions were included already densely in public consciousness and most often associate with recognition of images and speeches, with generation of the humanoid text. Actually algorithms Machine training can solve a set of various types of tasks, including help small business, to the Internet edition and anything. In this article I will tell as to create Neural networks who is capable to solve a real business challenge on creation of skoringovy model. We will consider all stages: from preparation of data before creation of model and an assessment of its quality.
Questions which are sorted in article:
• How to collect and prepare the models given for construction?
• What is Neural networks and how it is arranged?
• How to write the Neural networks from scratch?
• How it is correct to train Neural networks on available data?
• How to interpret model and its results?
• How it is correct to estimate quality of model?
"A question of, whether can think the computer, is no more interesting,
than a question of, whether the submarine" can float.
Edsger Vibe Dijkstra
In many companies, sales managers communicate with potential clients, hold demonstrations them, tell about product. Give, so to speak, the soul on the 100-th time on worry by that who, probably, fell into their hands absolutely incidentally. Often clients understand insufficiently that it is necessary for them, or that product can give them. Communication with such clients does not bring pleasures, arrived. And the most unpleasant that because of restriction on time, it is possible not to pay enough attention to really important client and to miss the transaction.
Ya the mathematician-programmer in the seo-analitiki Serpstat service. Recently I received an interesting task of improvement of skoringovy model already existing and working for us, having in a new way estimated factors which influence success of sale. Scoring was considered on the basis of questioning of our clients, and each point, depending on the answer to a question, brought a certain quantity of points in total point. All these points for different questions were placed on the basis of statistical hypotheses. The Skoringovy model was used, time went, data gathered and one fine day got to me. Now, when I had a sufficient selection, it was possible to build safely hypotheses, using algorithms Machine training. I will tell
Ya to you as we constructed the scoring model. It is a real case with real data, with all difficulties and restrictions which we met in real business. So, about everything one after another.
We will in detail stop at all stages of work:
▸ Data collection
▸ Preprocessing
▸ Creation of the
model ▸ the Analysis of quality and interpretation of the
model
we Will consider the device, creation and training of Neural networks. I describe all this, solving a real skoringovy problem, and constantly I support the new theory with an example.
need to be understood In the beginning Data collection, what questions will represent the client (or simply object) in future model. We approach to a task seriously as on its basis further process is based. First, it is necessary not to miss the important signs describing object, secondly, to create rigid criteria for decision-making on a sign. Based on experience, I can allocate three categories of questions:
- Boolean (bikategorialny), the answer on which is: Yes or no (1 or 0). For example, answer to a question: whether there is at the client an account?
- Categorial, the answer on which is the concrete class. Usually classes of more than two (multicategorial), differently the question can be reduced to the Boolean. For example, color: red, green or blue.
- Quantitative, answers on which are the numbers, characterizing a concrete measure. For example, number of addresses in a month: fifteen.
Why I so in detail stop on it? Usually, when consider the classical task solved by algorithms Machine training, we deal only with numerical data. For example, recognition of black-and-white hand-written figures from the picture 20 on 20 pixels. In this example of 400 numbers (describing brightness of black-and-white pixel) represent one example from selection. Generally data optional have to be numerical. The matter is that at creation of model it is necessary to understand, with what types of questions the algorithm can deal. For example: the tree of decision-making is trained on all types of questions, and Neural networks accepts only numerical entrance data and is trained only on quantitative signs. Whether means it, what we have to refuse some questions to please more perfect model? At all not, it is just necessary to prepare data correctly.
Data have to have the following classical structure: vector of signs for each i-go of the client of X (i) = { x (i) 1 , x (i) 2 ... x (i) to n } and the class Y (i) — the category, showing were bought by him or not. For example: the client (3) = { green, bitter, 4.14 and } — bought. to
based on the aforesaid, we will try to present a format of the questions given with types, for further preparation:
| class: (category) of | color: (category) of | taste: (category) of | weight: (number) of | firm: (bool) of |
|---|---|---|---|---|
| - | red | sour | 4.23 | yes |
| - | green | bitter | 3.15 | is not present |
| %2B | green | bitter | 4.14 | yes |
| %2B | blue | sweet | 4.38 | is not present |
| - | green | 3.62 | there is no Table 1 |
— the Example of data of training selection before preprocessing
Preprocessing
After data are collected, they need to be prepared. This stage is called preprocessing. The main objective of preprocessing — display of data in a format suitable for model training. It is possible to allocate three main manipulations over data at a preprocessing stage:
- Creation of vector space of signs where there will live examples of training selection. In fact, it is process of reduction of all data in a numerical form. It relieves us from category, Boolean and other not numerical types.
- Normalization of data. Process at which we achieve, for example that average value of each sign according to all available information was zero, and dispersion — single. Here the most classical example of normalization of data: X = (X — μ)/σ
function of normalizationof def normalize (X): return (X-X.mean()) / X.std () - Change of dimension of vector space. If the vector space of signs is too great (million signs) or few (less than ten), it is possible to apply methods of increase or fall of dimension of space:
- For increase of dimension can use part of training selection as reference points , having added in a vector of signs distance to these points. This method often leads to that in spaces of higher dimension of a set become linearly razdelimy, and it simplifies a problem of classification.
- For dimension fall most often are used by PCA. The main objective a method main a component — search of new linear combinations of signs along which dispersion of values of projections of elements of training selection is maximized.
One of the major tricks in creation of vector space — a representation method in the form of number of categorial and Boolean types. Meet: One-Hot (Russian. Unitary Code). The main idea of such coding — this representation of a categorial sign, as vector in vector space the dimension corresponding to amount of possible categories. Thus value of coordinate of this category undertakes unit, and all other coordinates are nullified. With Boolean values everything is absolutely simple, they turn into material units or zero.
For example, a sample unit can be either bitter, or sweet, either salty, or sour, or minds (meat). Then One-Hot the coding will be following: bitter = (1, 0, 0, 0,0), sweet = (0, 1, 0, 0,0), salty = (0, 0, 1, 0,0), sour = (0, 0, 0, 1,0), minds = (0, 0, 0, 0, 1). If you had a question why tastes five, instead of four, examine this article about flavoring touch system , well and it has no relation to scoring, and we will use four, having limited to old classification.
Now we learned to turn categorial signs in usual numerical a vector, and it is very useful. Having carried out all manipulations over data, we will receive the training selection suitable any model. In our case, after application of the unitary coding and normalization data look so:
| class: | red: | green: | blue: | bitter: | sweet: | salti: | sour: | weight: | solid: |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0.23 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | -0.85 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0.14 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0.38 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | -0.48 |
Can tell
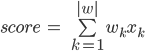
Where, k — is question number in the questionnaire, w k — coefficient of a contribution of the answer to this k-y a question in total scoring, |w | — quantity of questions (or coefficients), x k — the answer to this question. Thus questions can be any as we and discussed: Boolean (yes or no, 1 or 0), numerical (for example, growth = 175) or categorial, but presented in the form of the unitary coding (green from the list: red, green or blue = [0, 1, 0]). Thus it is possible to consider that categorial questions break up on so much Boolean, how many categories are present at versions of the answer (for example: client red? client green? client blue? ) .
model
Now the most important: model choice. Today there is a set of algorithms Machine training on the basis of which it is possible to construct scoring model: Decision Tree (decision tree), KNN (method of the k-next neighbors), SVM (method of basic vectors), NN (Neural networks), TV channel "CNN" (svertochny Neural networks). And the choice of model should be based on what we want from it. First, as far as the decisions which have affected results of model, have to be clear. In other words, as far as it is important to us to have opportunity to interpret model structure.
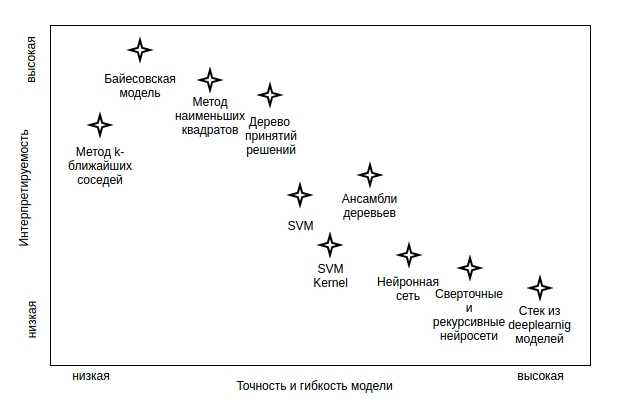
of Fig. 1 — Machine training and interpretiruyemost of the received
Besides, not all models it is easy for
to construct Dependence of flexibility of algorithm, for some very specific skills and very much powerful iron are required. But the most important — this introduction of the constructed model. Happens so that business process is already adjusted, and introduction of any difficult model is simply impossible. Or linear model in which clients, answering questions is required, get positive or negative points depending on version of the answer. Sometimes, on the contrary, there is a possibility of introduction, and even the difficult model considering very unevident combinations of input parameters, finding interrelations between them is required. So, what to choose?
In a choice of algorithm Machine training we stopped on Neural networks. Why? First, now there are many abrupt frameworks, such as TensorFlow, Theano. They give the chance very deeply and to adjust architecture and training parameters seriously. Secondly, opportunity to change the model device from single-layer Neural networks which, by the way, is not bad interpreted, to multilayered, possessing excellent ability to find nonlinear dependences, changing thus only couple of lines of a code. Besides, the trained single-layer Neural networks can be turned into classical additive scoring the model putting points for answers to different questions of questioning, but about it a bit later.
is a little Now theory. If for you such things as neuron, activation function, loss function, gradient descent and a method of the return distribution of a mistake — native words, can safely pass it everything. If is not present, welcome to a short course of Neural networks. Short course of Neural networks
we Will begin
with that Neural networks (INS) — are mathematical models of the organization of real biological Neural networks (BNS). But unlike the BNS, INS mathematical models the exact description of all chemical and physical processes, such as the description of "firing" of the action potential (AP), work of neuromediators, ionic channels, secondary intermediaries, proteins of conveyors and so forth does not demand. From INS similarity with work of real BNS only on functional, instead of at physical level is required.
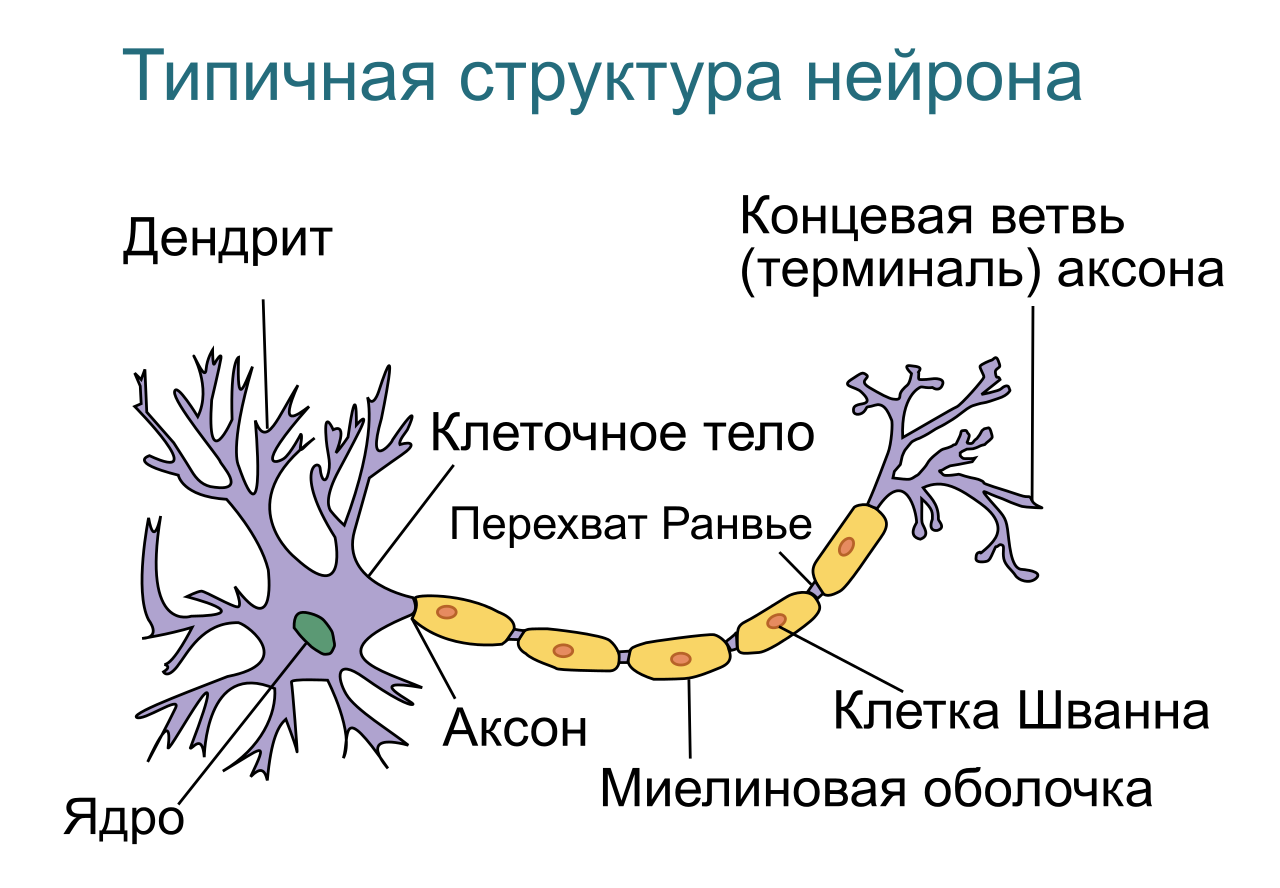
Basic Element of Neural networks — neuron. Let's try to make the simplest functional mathematical model of neuron. For this purpose we will sketch functioning of biological neuron.
of Fig. 2 — Typical structure of biological neuron
As we see
 and Walter Pitts in 1943 offered model of mathematical neuron. And in 1958 Rozenblatt Frenk on the basis of neuron Warren Mak-Kallok - Kalloka-Walter Pitts created the computer program, and then and the physical device — a perceptron. The history of Neural networks. Now we will consider structural model of neuron with which we will deal further.
and Walter Pitts in 1943 offered model of mathematical neuron. And in 1958 Rozenblatt Frenk on the basis of neuron Warren Mak-Kallok - Kalloka-Walter Pitts created the computer program, and then and the physical device — a perceptron. The history of Neural networks. Now we will consider structural model of neuron with which we will deal further.

of Fig. 3 — Model of mathematical neuron Warren Mak-Kallok - Kalloka-Walter Pitts
Where:
- X — an entrance vector of parameters. Vector (column) of numbers (biol. extent of activation of different receptors), come to an entrance to neuron.
W — a vector of scales (generally — a matrix of scales), numerical value which change in the course of training (biol. training on the basis of synoptic plasticity, neuron learns to react correctly to signals from its receptors). - the Adder — the functional block of neuron which puts all input parameters increased on corresponding to them weight.
- Function of activation of neuron — is dependence of value of an exit of neuron on value of the comer on the adder.
- the Following neurons where on one of a set of their own entrances value from an exit of this neuron (this layer moves can be absent, if this neuron the last, terminal).
realization of mathematical neuron of import numpy as np def neuron (x, w) : z = np.dot (w, x) output = activation (z) return output
Then from these minimum structural units collect classical Neural networks. The following terminology is accepted:
- the Entrance (receptor) layer — is a vector of parameters (signs). This layer does not consist of neurons. It is possible to tell that it is the digital information removed by receptors from the "external" world. In our case it is information on the client. The layer contains so many elements, how many input parameters (bias-term plus necessary for shift of a threshold of activation).
- the Associative (hidden) layer — the deep structure capable to storing of examples, to finding of difficult correlations and nonlinear dependences, to creation of abstractions and generalizations. Generally it at all a layer, and a set of layers between entrance and output. It is possible to tell that each layer prepares new (more high-level) vector of signs for the following layer. This layer is responsible for emergence in the course of training of high-level abstractions. The structure contains so many neurons and layers, to the top of the bent, and maybe in general to be absent (in case of classification of linearly razdelimy sets).
- the Output layer — is the layer which each neuron is responsible for a concrete class. Different classes can interpret an exit of this layer as function of distribution of probability of accessory of object. The layer contains so many neurons, how many classes are presented in training selection. If class two, it is possible to use two output neurons or to be limited to only one. In that case one neuron still is responsible only for one class but if it gives out values close to zero, the sample unit on its logic has to belong to other class.
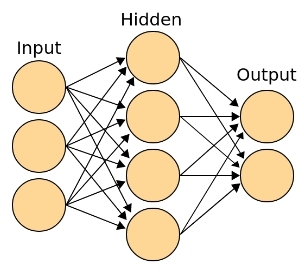
of Fig. 4 — Classical topology of Neural networks, with entrance (receptor), to the days off making the decision on a class, and the associative (hidden) layer
Exactly thanks to existence of the hidden associative layers, Neural networks is capable to build the hypotheses based on finding of difficult dependences. For example, for svertochny Neural networks, distinguishing images, on an entrance layer values of brightness of pixels of the image will move, and the output layer will contain the neurons which are responsible for concrete classes (the person, the car, a tree, the house etc.) In the course of training in the hidden layers close to "receptors" will start "by itself" appearing (to specialize) the neurons which are exciting from straight lines, a different tilt angle, then reacting to corners, squares, circles, primitive patterns: alternating strips, geometrical mesh ornaments. Closer to output layers — the neurons reacting, for example, approximately, a wheel, a nose, a wing, a leaf, the person etc.

of Fig. 5 — Education hierarchical associations in the course of training svertochny Neural networks
Drawing a biological analogy, Dubynin Vyacheslav , concerning speech model want to refer to words of the remarkable neurophysiologist:
"Our brain is capable to create, generate such words which generalize words of lower level. Let's tell, the hare, a ball, cubes, a doll ― toys; toys, clothes, furniture ― it is subjects; and subjects, at home, people ― it is objects of environment. And it is so a little more, and we will reach abstract philosophical concepts, mathematical, physical. That is speech generalization ― this very important property of our associative parietal bark, and it, in addition, multilevel also allows to form speech model of the outside world, as integrity. At some instant it appears that nervous impulses are capable to move very actively on this speech model, and we and call this movement the proud word "thinking".
it is A lot of theory? ! But there are also good news: in the simplest case all Neural networks can be presented by the unique neuron! Thus even one neuron often well copes with a task, especially, when business concerns recognition of a class of object in space in which objects of these classes are linearly separabelny. Often it is possible to achieve linearly separability having increased dimension of space about what it was written above, and to be limited to only one neuron. But it is sometimes simpler to add in Neural networks couple of hidden layers and not to demand from selection of linear separability.
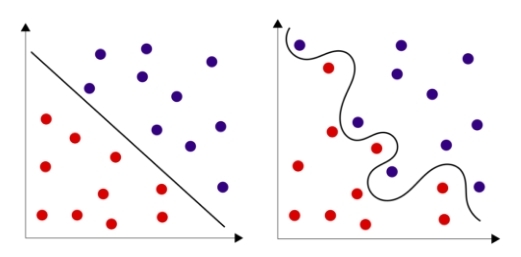
of Fig. 6 — Linearly razdelimy sets and linearly inseparable sets
Well and now let's describe all this formally. On a neuron entrance we have a vector of parameters. In our case it is results of questioning of the client, presented in the numerical form X (i) = { x (i) 1 , x (i) 2 ... x (i) n }. Thus Y (i) — the class characterizing success of a lead (1 or 0) is compared to each client. Neural networks, in fact, has to find optimum dividing hypersurface in the vector space which dimension corresponds to quantity of signs. Training Neural networks in that case — finding of such values (coefficients) of a matrix of scales of W at which the neuron which is responsible for a class, will give out values close to unit in those cases if the client buys, and values close to zero if is not present.
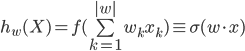
Apparently from a formula, result of work of neuron — is activation function (often designated through) from the sum of work of input parameters on required in the course of training coefficients. Let's understand that such activation function.
As on an entrance of Neural networks can arrive any valid values, and coefficients of a matrix of scales too can be any, and any real number from a minus to infinity plus can be result of the sum of their works. Each element of training selection has a value of a class concerning this neuron (zero or one). It is desirable to receive from neuron value in the same range from zero to unit, and to make the decision on a class, depending on to what this value is closer. It is even better to interpret this value as probability of that the element belongs to this class. Means, such monotonous smooth function which will display elements from a set of real numbers in area from zero to unit is necessary to us. To this position perfectly approaches so-called sigmoida.
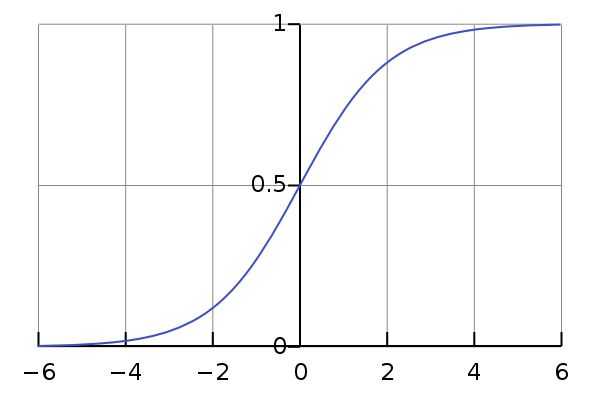
of Fig. 7 — the Schedule of the logistic curve, one of the most classical representatives of a class sigmoid
function of activation of def activation (z): return 1 / (1%2Bnp.exp (-z))
By the way, in real biological neurons such continuous function of activation was not realized. In our cages there is a potential of rest which averages - 70mV. If on neuron information, the activated receptor moves, opens the ionic channels interfaced to it that leads to increase or potential fall in a cage. It is possible to draw an analogy between force of reaction to activation of a receptor and one coefficient of a matrix of scales received in the course of training. As soon as potential reaches value in - 50mV, there is PD, and the wave of excitement reaches on an axon the presinaptichesky termination, throwing out a neuromediator on mezhsinaptichesky Wednesday. That is real biological activation — step, instead of smooth: the neuron either was activated, or is not present. It shows as far as we are mathematically free in creation of our models. Having taken from the nature the basic principle of the distributed calculation and training, we are capable to construct the computing count consisting of elements, possessing any desirable properties. In our example we wish to receive from neuron continual, instead of discrete values. Though generally function of activation can be and another.
Here the most important that it is worth taking from written above: "Training of Neural networks (synoptic training) has to be reduced to optimum selection of coefficients of a matrix of scales for the purpose of minimization of a made mistake. " in case of single-layer Neural networks these coefficients can be interpreted as a contribution of parameters of an element to probability of belonging to a concrete class.
can call Result of work of Neural networks were true (to real classes of objects) as much as possible. Actually here the main idea of training on experience also is born. Now we will need the measure describing quality of Neural networks. This functionality usually call "function of losses" (English loss function). Functionality usually designate through J(W), showing its dependence on coefficients of a matrix of scales. The functionality is less, the more rare ours Neural networks is mistaken and it is better for those. To minimization of this functionality training also is reduced. Depending on coefficients of a matrix of scales Neural networks can have different accuracy. Training process — this movement on hypersurface of functionality of the loss which purpose is minimization of this functionality.
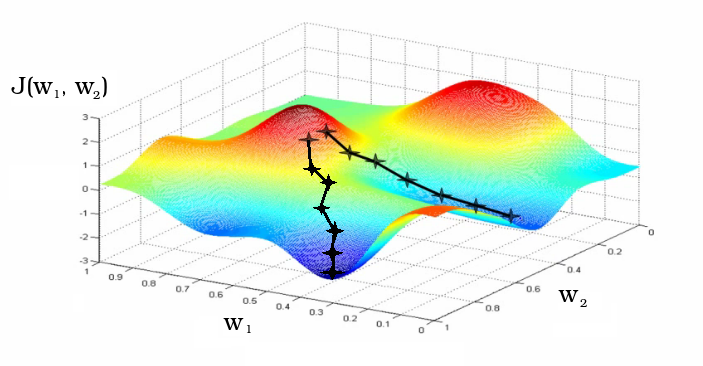
of Fig. 8 — training Process as gradient descent to a local minimum of functionality of loss Usually coefficients of a matrix of scales are initialized by
in a random way. In the course of training coefficients change. On graphics two different iterative ways of training as change of coefficients of w 1 and w 2 matrixes of scales of Neural networks, initialized in the neighbourhood are shown.
Now actually how to train Neural networks. For this purpose there is a set of options, but I will tell about two: evolutionary (genetic) algorithm and method of gradient descent. Both of these methods are used. Evolutionary algorithms — this direction in Artificial intelligence which is based on modeling of natural selection. The evolutionary method of training is very simple in understanding, and it is better for beginners to begin with it. Now it is used generally for training of deep layers of Neural networks. Method of gradient descent and return distribution of a mistake more difficult, but one of the most effective and popular methods of training.
Evolutionary training
Within this method we operate with the following terminology: coefficients of a matrix of scales — the genome, one coefficient — a gene, "turned headfirst" function of losses — a fitness landscape (here we already look for a local maximum, but it only convention). This method indeed the very simple. After we chose topology (device) of Neural networks, it is necessary to make sleduyushcheye:
- Proinitsializirovat a genome (a matrix of scales) in a random way in the range from-1 to 1. To repeat it several times, having thereby created initial population different, but casual Neural networks. We will designate the size of population through P — population or parents.
casual initialization of coefficients of a matrix of scales of import random def generate_population (p, w_size): population = [] for i in range (p): model = [] for j in range (w_size %2B 1): %23%2B1 for b (bias term) of model.append (2 * random.random () - 1) %23 random initialization from-1 to 1 for b and w population.append (model) of return np.array (population)
- to Create several descendants. For example, three-four clones of each parent, having made little changes (mutations) to their genome. For example: to renominate in a random way a half of scales, or to add in a random way to a half of scales casual values in the range from-0.1 to 0.1.
realization of a mutagenesis of def mutation (genom, t=0.5, m=0.1): mutant = [] for gen in genom: if random.random ()
- to Estimate fitness of each descendant, how it copes with examples from training selection (in the simplest option — percent of truly guessed classes, in an ideal — the turned function of losses). To sort descendants by their fitness.
the simplest assessment of fitness of def accuracy (X, Y, model): A = 0 m = len(Y) for i, y in enumerate (Y): %2B = (1/m) * (* (> = 0.5 else 0) %2B (1-y) * (0 if neuron (X [i], model)> = 0.5 else 1)) return A
- "To leave A to y by 1 if neuron (X [i], model) in live" only P of the most adapted. And to return to point 2, repeating this cycle several times. For example: hundred times or while accuracy does not become 80%.
realization of selection of def selection (offspring, population): offspring.sort () population = [kid[1] for kid in offspring [: len(population)]] return population
realization of evolutionary algorithm of def evolution (population, X_in, Y, number_of_generations, children): for i in range (number_of_generations): X = [[1] %2B [v.tolist ()] for v in X_in] offspring = [] for genom in population: for j in range (children): child = mutation(genom) child_loss = 1 - accuracy (X_in, Y, child) %23 or child_loss = binary_crossentropy (X, Y, child) is better offspring.append ([child_loss, child]) population = selection (offspring, population) return population
Such neuroevolution it is possible to improve. For example, it is possible to enter additional genes parameters, as τ — rate of a mutagenesis and μ — mutagenesis force. Now additive mutations in a matrix of scales of neurons will be is brought about probability τ, adding each parameter a random number in the chosen range (for example from-0.1 to 0.1) increased on μ. These genes too will be subject to variability.
In an ideal, selection has to control force and rate of a mutagenesis at different stages of evolution, increasing these parameters until jump it is possible to get out of a local maximum of a landscape of fitness, or reducing them that slowly and without sharp jumps to move to a global maximum. It is also possible to add in model a krossingover. Now descendants will be formed by crossing, having received in a random way on a half of genes from two casual parents. In this scheme too it is necessary to leave entering of casual mutations into a genome. Here I deem it to cite
appropriate the book Markov Alexander and Naymark Helena:
"Harmful mutations — this movement downhill, useful — a way upward. Mutations neutral, not influencing fitness, correspond to movement along horizontals — lines of identical height. Rejecting the harmful mutations, natural selection prevents evolving sequence to move down on a fitness landscape. Supporting mutations useful, selection tries to tire out sequence as it is possible above. "
Gradient descent and a method of the return distribution of a mistake
If the following material will be difficult for understanding, return to it later. Besides a set of libraries Machine training give the chance to realize with ease training by this method, without going into details. When we take a root, using the calculator, us usually as it it interests does a little, we perfectly know that we want to receive, and we give the account to the car. But this method is interesting to those to whom, we will review it briefly. we Will begin
with that one output neuron in our model is responsible only for one class. If it is object of that class for which the neuron is responsible, we wish to see unit at its exit, otherwise — zero. In a real prediction of a class as we already know, the artificial neuron is activated in the open range between zero and unit, thus value can be as much as close to these two asymptotes. Means, the more precisely we guess a class, the less absolute difference between a real class and activation of the neuron which is responsible for this class.
we Will try to create function of loss which would return numerical value of a penalty, such that it was small in that case when Neural networks gives out values close to value of a class, and very big in that case in which Neural networks gives out the values leading to the wrong definition of a class.
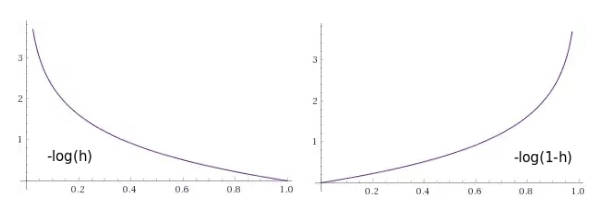
of Fig. 9 — Function graphs of penalties, as functions from a neuron exit: 1) in that case if the object belongs to this class (we expect unit), 2) in that case if object does not belong to this class (we expect zero)
needed to write down Now loss function in the form of expression. Once again I will remind that Y for each i-go of an element of training selection by the size m always accepts values or zero, or one so in expression always there will be only one of two members.
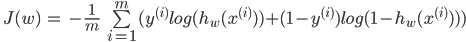
Those who is familiar with information theory, learn in this expression cross entropy (English cross entropy). From the point of view of the theory of information, training is minimization of cross entropy between real classes and model hypotheses.
function of loss of def binary_crossentropy (X, Y, model): %23 loss function J = 0 m = len(Y) for i, y in enumerate (Y): J %2B = - (1/m) * (y*np.log (neuron (X [i], model)) %2B (1. - y)*np.log (1. - neuron (X [i], model))) return J
Having initialized coefficients of a matrix of scales in a random way, we want to make to them changes which will make our model better, or being in a different way expressed, will reduce loss. If it is known as far as influence weight function of losses, it will be known as far as they need to be changed. Here we will be helped by a private derivative — a gradient. It shows how function depends on her arguments. On how many (midget) sizes it is necessary to change argument that function changed at one (midget) size. Means, we can pereinitsializirovat a matrix of scales as follows:
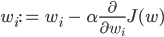
need to Repeat this step it is iterative. In fact, it also is gradual gradient descent by small short steps, of the size of α (this parameter still call rate of training), in a local minimum of functionality of loss. In other words, in each point which is set by present values W, we learn the direction in which the functionality of loss changes in the fastest way, and dynamics of training reminds the ball which is gradually rolling down in a local minimum.
gradient descent of def gradient_descent (model, X_in, Y, number_of_iteratons=500, learning_rate=0.1): X = [[1] %2B [v.tolist ()] for v in X_in] m = len(Y) for of it in range (number_of_iteratons): new_model = [] for j, w in enumerate (model): error = 0 for i, x in enumerate(X): error %2B = (1/m) * (neuron (X [i], model) - Y[i]) * X [i] [j] of w_new = w - learning_rate * error new_model.append (w_new) of model = new_model model_loss = binary_crossentropy (X, Y, model) return model
the Method of the return distribution of a mistake continues this chain of reasonings on a case multilayered Neural networks. Thanks to it it is possible to train deep layers on the basis of gradient descent. Training happens step by step from the last layer to the first. I think that this information quite will suffice to understand an essence of this method. Example of training of Neural networks
we Will assume
, we want to learn probability of purchase of the client on the basis of only one parameter — its age. We want to create neuron which will be excited when the probability of purchase makes more than 50%.
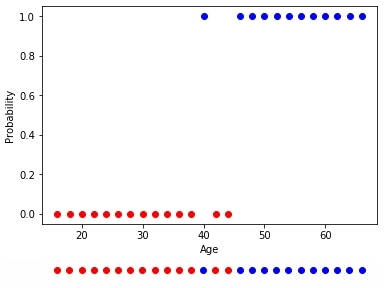
of Fig. 10 — Training selection bought and not bought
Means, the neuron has one receptor connected with age of the client. Besides, we add one bias the member who will be responsible for shift. For example, though these sets also are linearly inseparable, but approximate border, being in a different way expressed, the best dividing hypersurface (in an one-dimensional case — a point), between them settles down at the age of 42 years.
Neural networks has to give values of probability of purchase less than 0.5 at age till 42 years, more than 0.5 for more adult clients. If to remember activation function, it returns values big 0.5 for positive arguments and smaller 0.5 for — negative. Means, opportunity to shift this function of activation on any threshold value is necessary. Thus we expect such speed of a change of function of activation which best of all would correspond to training selection as from coefficients of a matrix of scales extent of excitement of each neuron as function will depend on a vector of signs x, and respectively probability of accessory of an element with such vector of signs to this class.
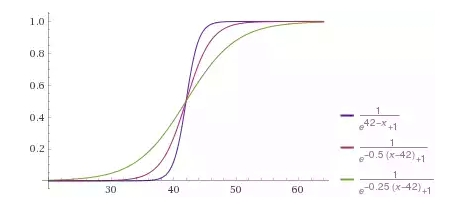
of Fig. 11 — Expected reaction of neuron to age of the client with different degree of "confidence" as a result, regulated in the coefficient at argument
Now we will write down it mathematically and we will understand, why one more bias-term in a matrix of scales is necessary to us. To displace function f (x) to the right, for example on 42, we have to subtract 42 of her argument of f (x-42). Thus we want to receive a weak excess of function, having increased argument, for example on 0.25, having received the following function f (0.25 (x-24)). Removing the brackets, we will receive:
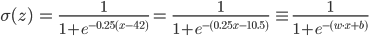
In our case required coefficient of a matrix of scales of w = 0.25, and b shift =-10.5. But we can consider that b is zero coefficient of a matrix of scales (w 0 =b) in case for any example unit (x 0 =1) is a zero sign always. Then, for example the fifteenth "vektorizirovanny" client with age in 45 years, presented as x (15) = { x (15) 0 , x (15) 1 } = [1, 30], could buy 68% with probability. Even in such simple example it is heavy to estimate all these coefficients "approximately". Therefore, actually, we also trust search of these parameters to algorithms Machine training. In our example we look for two coefficients of a matrix of scales (w 0 =b and w 1 ).
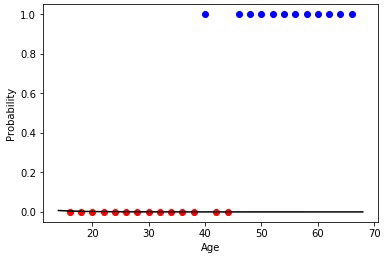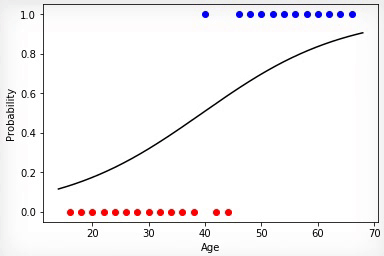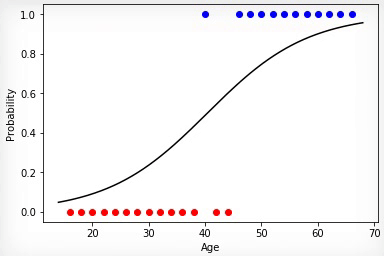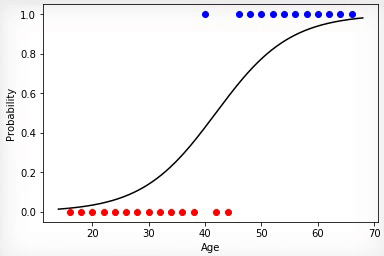
Animation 1 — Evolutionary training on data without normalization
Having initialized coefficients of a matrix of scales in a random way and having used evolutionary algorithm, we received the trained Neural networks after change of hundred generations. To receive the necessary result of training quicker and without such sharp jumps, it is necessary to normalize data before training.
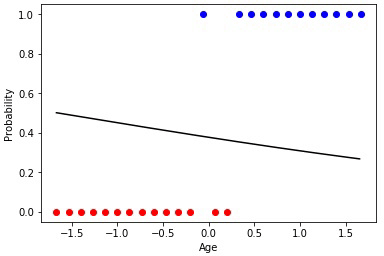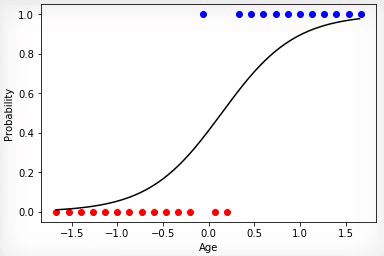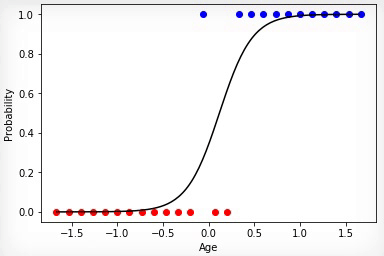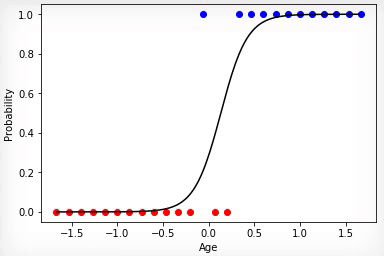
Animation 2 — Evolutionary training on rated data
Most precisely works a method of gradient descent. When using this method data always have to be normirovany. Unlike evolutionary algorithm the method of gradient descent does not experience jumps connected with "mutations", and gradually moves to an optimum. But the minus that this algorithm can get stuck in a local minimum and not to leave any more it or the gradient can "disappear" practically and training will stop.
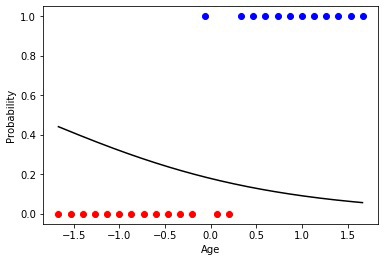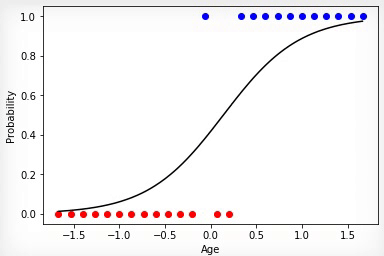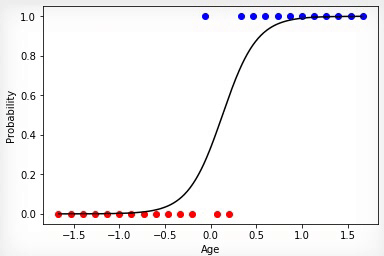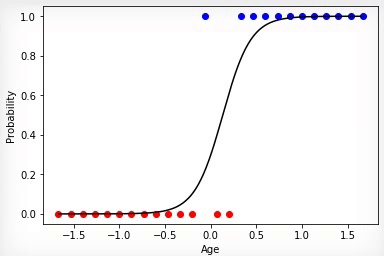
Animation 3 — Training on the basis of a method of gradient descent
In that case if sets of classes bought and not bought linearly razdelimy, neuron will "be more confident" in the decisions and change of extent of its activation will have more expressed change on border of these sets.
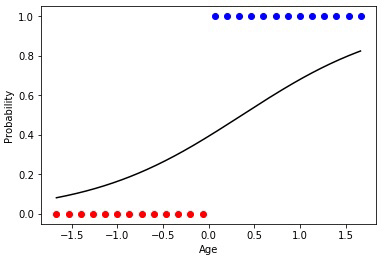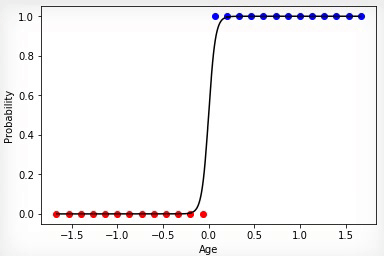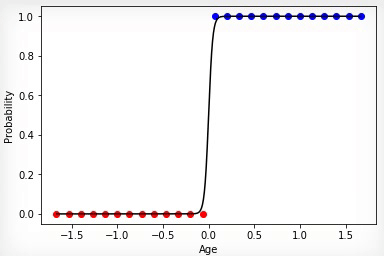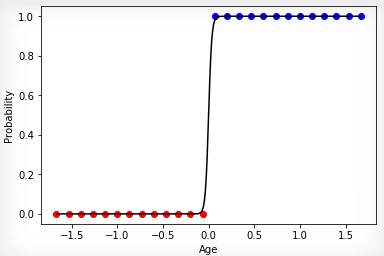 Animation 4 — Training on linearly razdelimy sets
Animation 4 — Training on linearly razdelimy sets
on the basis of considered can present to
a classical Neural networks in the form of the computing count containing:
- entrance tops x;
- of top which are neurons with values of their exit of a;
- of top which are responsible for bias b;
- of an edge multiplying values of an exit of the previous layer by coefficients corresponding to them of a matrix of scales of w;
- h w, b (x) — result of an exit of the last layer.
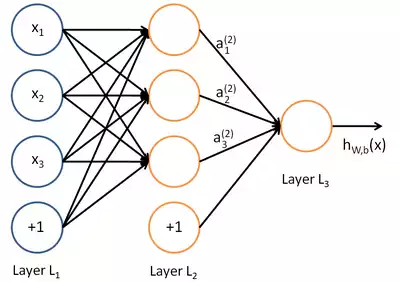
of Fig. 12 — the Computing count classical Neural networks
we Will review couple of examples online of a sandbox of library TensorFlow . In all examples it is necessary to divide two classes which objects settle down on the plane. The entrance layer has two "receptors" which values correspond to object coordinates on abscissa axes and ordinates (plus one bias, in animation of bias is not represented). As it was told, for training on linearly razdelimy sets it is enough to have only one output neuron, the hidden (associative) layer is absent. Training happens on the basis of a method of the return distribution of a mistake.
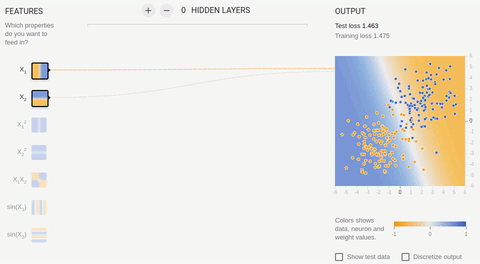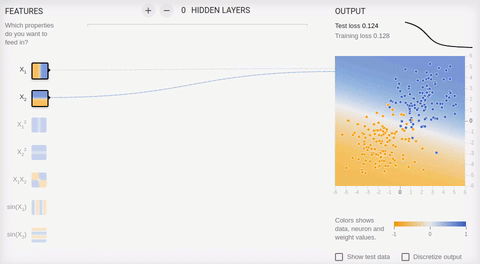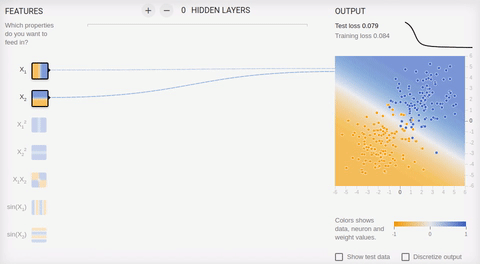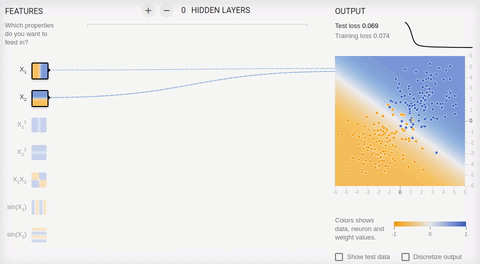
Animation 5 — One output neuron finds dividing straight line
we Will try to complicate a task and to divide sets, elements first of which have only positive or only negative values on both coordinates, and elements of the second have one positive and one negative value of their coordinates. In this example not to manage any more one dividing straight line therefore we will need existence of the hidden layer. Let's try to begin with the minimum and to add two neurons in the hidden layer.
Animation 6 — Two associative neurons and two dividing straight lines
As we see
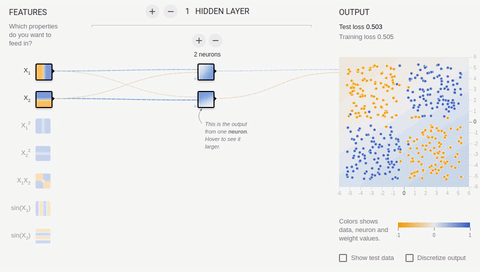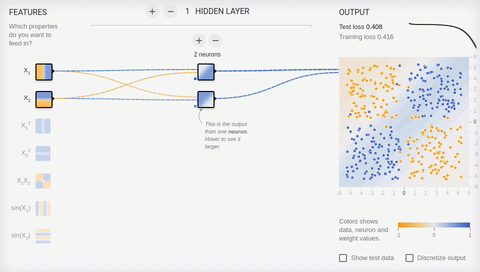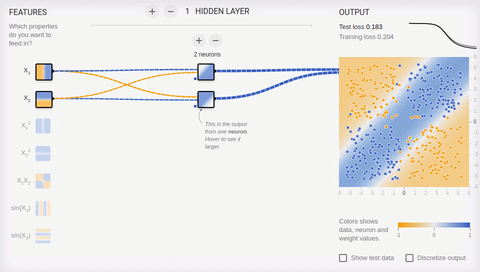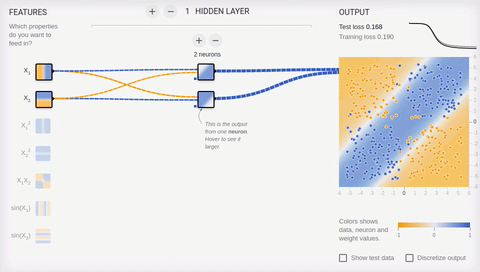
Animation 7 — Four associative neurons and four dividing straight lines
Neural networks well coped with this task. Pay attention to how there is a training. At first Neural networks found the simplest solution — dividing corridor. Then there was a respecialization of neurons. Now each hidden (associative) neuron is responsible for the narrow segment.
we Will try to solve rather complex problem — division of elements of two sets lying in different spiral sleeves.
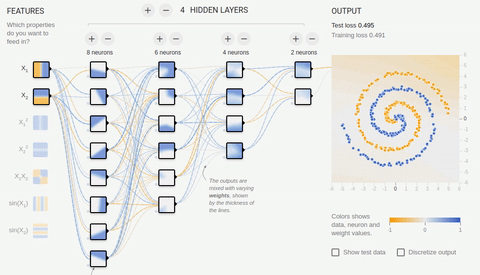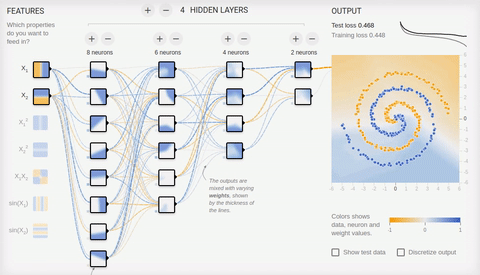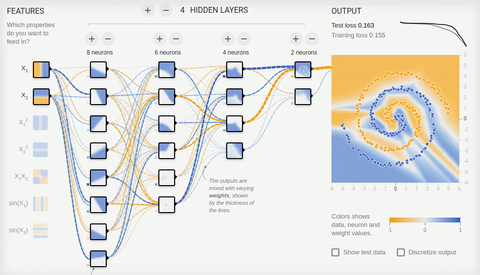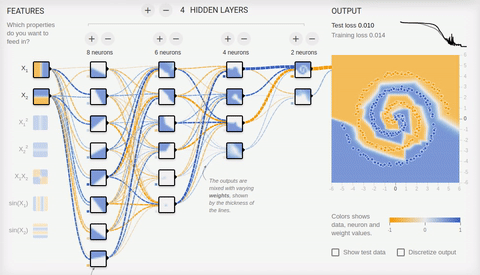 Animation 8 — the Multilayered Neural networks with topology "a bottle neck" to
Animation 8 — the Multilayered Neural networks with topology "a bottle neck" to
For the solution of a complex challenge is necessary for
a set of the hidden layers. With a task Neural networks well copes with topology "a bottle neck" in which the quantity of neurons decreases from the first hidden layer to the last. Pay attention to what difficult patterns arise at specialization of associative neurons. In case of deep Neural networks it is better to use ReLU (rectified linear unit) activation function for the hidden neurons, and usual logistic activation (in an ideal softmax - activation) for the last layer.
On it, I think, it is possible to finish our supershort course of Neural networks, and to try to put our knowledge into practice. I advise to construct the model on already ready library which now are for any programming language, and also gradually to deepen the theoretical knowledge in this direction.
model
When at us is both training selection, and theoretical knowledge, we can begin training of our model. However the problem is that often elements of sets are presented in unequal proportions. The bought there can be 5%, and not bought — 95%. How in that case to make training? After all it is possible to achieve 95% of reliability, claiming that nobody will buy.
Probably, an accuracy metrics in that case has to be other and it is necessary to train too reasonably that Neural networks did not draw the same obviously incorrect conclusion. For this purpose I suggest "to feed" Neural networks with the training examples containing equal quantity of elements of different classes.
For example if we have only 20,000 examples and from them 1,000 bought, it is possible to choose in a random way from each group on 500 examples and to use them for training. And to repeat this operation over and over again. It complicates realization of process of training a little, but helps to receive competent model. by
Having chosen model and algorithm of training, it is desirable to divide your selection into parts: to provide training on the training selection making 70% of everything, and to offer 30% for test selection which is required for the analysis of quality of the received model.
the Assessment of quality of model
Having prepared model, it is necessary to estimate adequately its quality. For this purpose we will enter the following concepts:
- of TP (True Positive) — istinopolozhitelny. The qualifier decided that the client will buy, and he bought.
- of FP (False Positive) — false positive. The qualifier decided that the client will buy, but he did not buy. It is a so-called error of the first sort. It is not so terrible, as an error of the second sort, especially when the qualifier — the test for any disease.
- of FN (False Negative) — lozhnootritsatelny. The qualifier decided that the client will not buy, and he could buy (or already bought). It is a so-called error of the second sort. Usually at creation of model it is desirable to minimize a mistake of the second, even having increased thereby an error of the first sort.
- of TN (True Negative) — istinootritsatelny. The qualifier decided that the client will not buy, and he did not buy.
Krom of a direct assessment of reliability as a percentage there are such metrics, as the accuracy (English precision) and completeness (English recall), based on the above-stated results of binary classification.
of Fig. 13 — Comparison of results of classification of different models
As we see
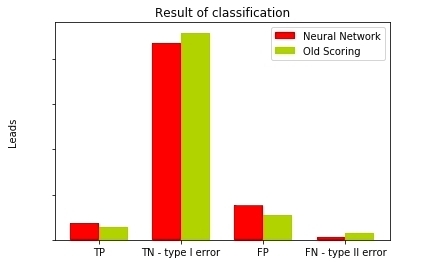 has three times a smaller error of the second sort in comparison with old scoring model, and it is very quite good. After all missing potential clients, we miss potential profit. Give now on the basis of available data we will remove metrics of quality of our models.
has three times a smaller error of the second sort in comparison with old scoring model, and it is very quite good. After all missing potential clients, we miss potential profit. Give now on the basis of available data we will remove metrics of quality of our models.
the Metrics of reliability
the simplest metrics — is a reliability metrics (English Accuracy). But this metrics should not be the only metrics of model as we already understood. Especially when there is a distortion in selection, that is representatives of different classes meet different probability.
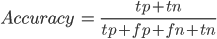
the Accuracy and completeness
the Accuracy (English precision) shows the attitude of truly guessed objects of a class to all objects which we defined as objects of a class. For example, we decided that will buy 115, and from them really bought 37, accuracy means makes 0.33. Completeness (English recall) shows the attitude of truly guessed objects of a class to all representatives of this class. For example, among us guessed really bought 37, and all bought was 43. Our completeness means makes 0.88.
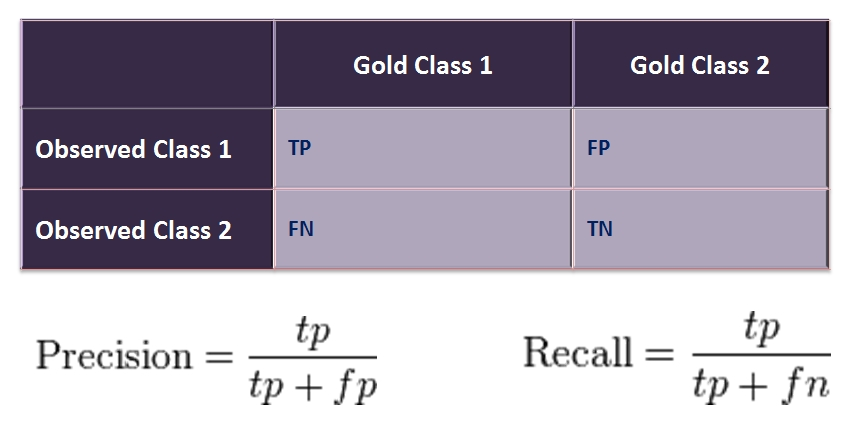
of Fig. 14 — the Table of mistakes or confusion matrix
a F-measure
Also exists a F-measure (English. F1 score) — an average of harmonious accuracy and completeness. Helps to compare models, using one numerical measure.
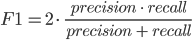
Using all these metrics, we will carry out an assessment of our models.
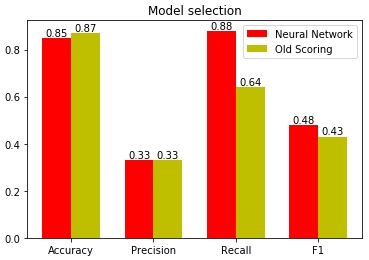
of Fig. 15 — the Assessment of quality of models on the basis of different statistical metrics
Apparently on the chart, the biggest distortion as models in a completeness metrics (English recall). Neural networks guesses 88% of potential clients, missing only 12%. Old scoring the model missed 36% of percent of potential clients, passing to managers only 64%. Here actually why it is better to entrust Neural networks to select coefficients of the importance of the different answers influencing scoring. After all the car is capable to keep all selection in the memory, to find in it regularities and to build the model possessing good predictive ability.
model
When at us is ready model, we can use it, expecting that accuracy to which to us gave the analysis of its quality. If there is an opportunity to introduce difficult (multilayered) model in the process, it is good but if is not present, it is possible to receive habitual scoring model from single-layer Neural networks. Exactly for this purpose we so in detail examined the device of Neural networks safely to glance it under a cowl.
we Will compare a formula linear scoring models and function of work of one neuron (or single-layer Neural networks):
we See
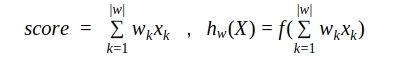 . Means, "having pulled out" values of a matrix of scales from single-layer Neural networks, we can use them as in coefficients scoring models. Only now these coefficients are picked accurately up by algorithm on the basis of a large number of data.
. Means, "having pulled out" values of a matrix of scales from single-layer Neural networks, we can use them as in coefficients scoring models. Only now these coefficients are picked accurately up by algorithm on the basis of a large number of data.
Now we will compare results linear scorings on the basis of coefficients before introduction of Neural networks. Let's remember that logistic function of activation gives value (from the point of view of Neural networks — probability of belonging to a class bought) bigger 0.5 at positive value of argument (scorings on the basis of a matrix of scales). We increased values neural scorings by hundred for the purpose of scaling of points and added five hundred as threshold value. At old scorings the threshold through passage was selected manually and made hundred seventy. All these simply linear manipulations which are not influencing in any way model.
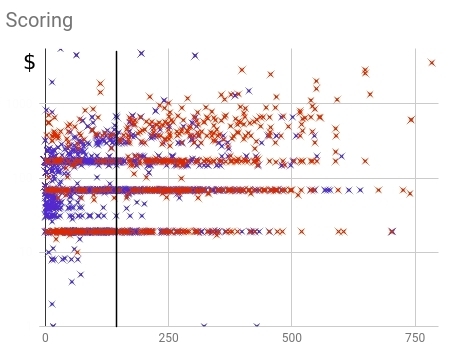
of Fig. 16 — Distribution of the bought (red) and not bought (blue) clients within old scoring models
Apparently from distribution, clients are too strongly smeared on all range of values scorings. Completeness (a share predicted by model) makes 64% of all number of the bought clients.
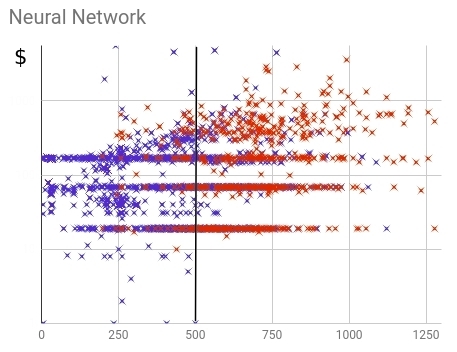
of Fig. 17 — Distribution of the bought (red) and not bought (blue) clients within neural scoring models
From distribution is visible that Neural networks coped with a problem of division of the bought and not bought users it is better than old model. Not bought, in the main weight, received values below threshold, bought — above. Completeness (a share predicted by model) makes 88% of all number of the bought clients.
Result
Solving our problem we wanted to find as much as possible time for those who will buy a tariff for a large sum. Besides, we wished to create such scoring model in which the clients buying the cheapest tariff, would not gather a lowest passing score.
This time for training Neural networks we divided selection into a class bought for a certain sum above, and on a class bought for the smaller sum or not not bought.
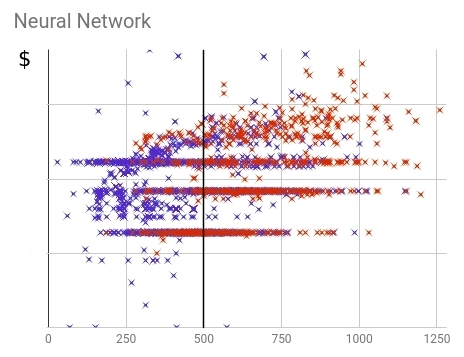
of Fig. 18 — Distribution of the bought (red) and not bought (blue) clients within final neural scoring models
At other, almost equal indicators of accuracy, Neural networks could achieve bigger completeness and could capture 87% bought expensive tariff plans. For comparison: old scoring consulted only from 77%. Means, in the future we will be able to cover another 10% of powerful and potential clients. Thus the percent bought expensive tariffs from last scoring is almost identical: 23% and 24% for Neural networks and old model respectively. Thus it is visible that value well correlates scorings with the purchase sum.
of Fig. 19 — Comparison of quality old and new scoring models
So, in this article we:
- Considered all main stages Data Mining.
- were Learned by many useful receptions both by preparation of data, and when training.
- Rather deeply got acquainted with the theory of classical Neural networks.
- were Considered by different statistical approaches to the analysis of quality of model.
- all stages from creation before analysis and introduction Described Neural networks on the example of construction linear scoring models.
- Showed how modern algorithms Machine training can help with the solution of real business challenges.
If you still had questions, wishes or remarks, let's discuss in comments.
W — a vector of scales (generally — a matrix of scales), numerical value which change in the course of training (biol. training on the basis of synoptic plasticity, neuron learns to react correctly to signals from its receptors).
of import numpy as np def neuron (x, w) : z = np.dot (w, x) output = activation (z) return output of def activation (z): return 1 / (1%2Bnp.exp (-z)) casual initialization of coefficients of a matrix of scales
of import random def generate_population (p, w_size): population = [] for i in range (p): model = [] for j in range (w_size %2B 1): %23%2B1 for b (bias term) of model.append (2 * random.random () - 1) %23 random initialization from-1 to 1 for b and w population.append (model) of return np.array (population) realization of a mutagenesis
of def mutation (genom, t=0.5, m=0.1): mutant = [] for gen in genom: if random.random () the simplest assessment of fitness
of def accuracy (X, Y, model): A = 0 m = len(Y) for i, y in enumerate (Y): %2B = (1/m) * (* (> = 0.5 else 0) %2B (1-y) * (0 if neuron (X [i], model)> = 0.5 else 1)) return A realization of selection
of def selection (offspring, population): offspring.sort () population = [kid[1] for kid in offspring [: len(population)]] return population of def evolution (population, X_in, Y, number_of_generations, children): for i in range (number_of_generations): X = [[1] %2B [v.tolist ()] for v in X_in] offspring = [] for genom in population: for j in range (children): child = mutation(genom) child_loss = 1 - accuracy (X_in, Y, child) %23 or child_loss = binary_crossentropy (X, Y, child) is better offspring.append ([child_loss, child]) population = selection (offspring, population) return population of def binary_crossentropy (X, Y, model): %23 loss function J = 0 m = len(Y) for i, y in enumerate (Y): J %2B = - (1/m) * (y*np.log (neuron (X [i], model)) %2B (1. - y)*np.log (1. - neuron (X [i], model))) return J of def gradient_descent (model, X_in, Y, number_of_iteratons=500, learning_rate=0.1): X = [[1] %2B [v.tolist ()] for v in X_in] m = len(Y) for of it in range (number_of_iteratons): new_model = [] for j, w in enumerate (model): error = 0 for i, x in enumerate(X): error %2B = (1/m) * (neuron (X [i], model) - Y[i]) * X [i] [j] of w_new = w - learning_rate * error new_model.append (w_new) of model = new_model model_loss = binary_crossentropy (X, Y, model) return model 
of Fig. 10 — Training selection bought and not bought
Means, the neuron has one receptor connected with age of the client. Besides, we add one bias the member who will be responsible for shift. For example, though these sets also are linearly inseparable, but approximate border, being in a different way expressed, the best dividing hypersurface (in an one-dimensional case — a point), between them settles down at the age of 42 years.
Neural networks has to give values of probability of purchase less than 0.5 at age till 42 years, more than 0.5 for more adult clients. If to remember activation function, it returns values big 0.5 for positive arguments and smaller 0.5 for — negative. Means, opportunity to shift this function of activation on any threshold value is necessary. Thus we expect such speed of a change of function of activation which best of all would correspond to training selection as from coefficients of a matrix of scales extent of excitement of each neuron as function will depend on a vector of signs x, and respectively probability of accessory of an element with such vector of signs to this class.

of Fig. 11 — Expected reaction of neuron to age of the client with different degree of "confidence" as a result, regulated in the coefficient at argument
Now we will write down it mathematically and we will understand, why one more bias-term in a matrix of scales is necessary to us. To displace function f (x) to the right, for example on 42, we have to subtract 42 of her argument of f (x-42). Thus we want to receive a weak excess of function, having increased argument, for example on 0.25, having received the following function f (0.25 (x-24)). Removing the brackets, we will receive:
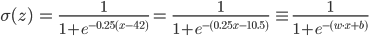
In our case required coefficient of a matrix of scales of w = 0.25, and b shift =-10.5. But we can consider that b is zero coefficient of a matrix of scales (w 0 =b) in case for any example unit (x 0 =1) is a zero sign always. Then, for example the fifteenth "vektorizirovanny" client with age in 45 years, presented as x (15) = { x (15) 0 , x (15) 1 } = [1, 30], could buy 68% with probability. Even in such simple example it is heavy to estimate all these coefficients "approximately". Therefore, actually, we also trust search of these parameters to algorithms Machine training. In our example we look for two coefficients of a matrix of scales (w 0 =b and w 1 ).

Animation 1 — Evolutionary training on data without normalization
Having initialized coefficients of a matrix of scales in a random way and having used evolutionary algorithm, we received the trained Neural networks after change of hundred generations. To receive the necessary result of training quicker and without such sharp jumps, it is necessary to normalize data before training.

Animation 2 — Evolutionary training on rated data
Most precisely works a method of gradient descent. When using this method data always have to be normirovany. Unlike evolutionary algorithm the method of gradient descent does not experience jumps connected with "mutations", and gradually moves to an optimum. But the minus that this algorithm can get stuck in a local minimum and not to leave any more it or the gradient can "disappear" practically and training will stop.

Animation 3 — Training on the basis of a method of gradient descent
In that case if sets of classes bought and not bought linearly razdelimy, neuron will "be more confident" in the decisions and change of extent of its activation will have more expressed change on border of these sets.
 Animation 4 — Training on linearly razdelimy sets
Animation 4 — Training on linearly razdelimy sets on the basis of considered can present to
a classical Neural networks in the form of the computing count containing:
- entrance tops x;
- of top which are neurons with values of their exit of a;
- of top which are responsible for bias b;
- of an edge multiplying values of an exit of the previous layer by coefficients corresponding to them of a matrix of scales of w;
- h w, b (x) — result of an exit of the last layer.

of Fig. 12 — the Computing count classical Neural networks
we Will review couple of examples online of a sandbox of library TensorFlow . In all examples it is necessary to divide two classes which objects settle down on the plane. The entrance layer has two "receptors" which values correspond to object coordinates on abscissa axes and ordinates (plus one bias, in animation of bias is not represented). As it was told, for training on linearly razdelimy sets it is enough to have only one output neuron, the hidden (associative) layer is absent. Training happens on the basis of a method of the return distribution of a mistake.

Animation 5 — One output neuron finds dividing straight line
we Will try to complicate a task and to divide sets, elements first of which have only positive or only negative values on both coordinates, and elements of the second have one positive and one negative value of their coordinates. In this example not to manage any more one dividing straight line therefore we will need existence of the hidden layer. Let's try to begin with the minimum and to add two neurons in the hidden layer.
Animation 6 — Two associative neurons and two dividing straight lines
As we see

Animation 7 — Four associative neurons and four dividing straight lines
Neural networks well coped with this task. Pay attention to how there is a training. At first Neural networks found the simplest solution — dividing corridor. Then there was a respecialization of neurons. Now each hidden (associative) neuron is responsible for the narrow segment.
we Will try to solve rather complex problem — division of elements of two sets lying in different spiral sleeves.
 Animation 8 — the Multilayered Neural networks with topology "a bottle neck" to
Animation 8 — the Multilayered Neural networks with topology "a bottle neck" to For the solution of a complex challenge is necessary for
a set of the hidden layers. With a task Neural networks well copes with topology "a bottle neck" in which the quantity of neurons decreases from the first hidden layer to the last. Pay attention to what difficult patterns arise at specialization of associative neurons. In case of deep Neural networks it is better to use ReLU (rectified linear unit) activation function for the hidden neurons, and usual logistic activation (in an ideal softmax - activation) for the last layer.
On it, I think, it is possible to finish our supershort course of Neural networks, and to try to put our knowledge into practice. I advise to construct the model on already ready library which now are for any programming language, and also gradually to deepen the theoretical knowledge in this direction.
model
When at us is both training selection, and theoretical knowledge, we can begin training of our model. However the problem is that often elements of sets are presented in unequal proportions. The bought there can be 5%, and not bought — 95%. How in that case to make training? After all it is possible to achieve 95% of reliability, claiming that nobody will buy.
Probably, an accuracy metrics in that case has to be other and it is necessary to train too reasonably that Neural networks did not draw the same obviously incorrect conclusion. For this purpose I suggest "to feed" Neural networks with the training examples containing equal quantity of elements of different classes.
For example if we have only 20,000 examples and from them 1,000 bought, it is possible to choose in a random way from each group on 500 examples and to use them for training. And to repeat this operation over and over again. It complicates realization of process of training a little, but helps to receive competent model. by
Having chosen model and algorithm of training, it is desirable to divide your selection into parts: to provide training on the training selection making 70% of everything, and to offer 30% for test selection which is required for the analysis of quality of the received model.
the Assessment of quality of model
Having prepared model, it is necessary to estimate adequately its quality. For this purpose we will enter the following concepts:
- of TP (True Positive) — istinopolozhitelny. The qualifier decided that the client will buy, and he bought.
- of FP (False Positive) — false positive. The qualifier decided that the client will buy, but he did not buy. It is a so-called error of the first sort. It is not so terrible, as an error of the second sort, especially when the qualifier — the test for any disease.
- of FN (False Negative) — lozhnootritsatelny. The qualifier decided that the client will not buy, and he could buy (or already bought). It is a so-called error of the second sort. Usually at creation of model it is desirable to minimize a mistake of the second, even having increased thereby an error of the first sort.
- of TN (True Negative) — istinootritsatelny. The qualifier decided that the client will not buy, and he did not buy.
Krom of a direct assessment of reliability as a percentage there are such metrics, as the accuracy (English precision) and completeness (English recall), based on the above-stated results of binary classification.
of Fig. 13 — Comparison of results of classification of different models
As we see
 has three times a smaller error of the second sort in comparison with old scoring model, and it is very quite good. After all missing potential clients, we miss potential profit. Give now on the basis of available data we will remove metrics of quality of our models.
has three times a smaller error of the second sort in comparison with old scoring model, and it is very quite good. After all missing potential clients, we miss potential profit. Give now on the basis of available data we will remove metrics of quality of our models. the Metrics of reliability
the simplest metrics — is a reliability metrics (English Accuracy). But this metrics should not be the only metrics of model as we already understood. Especially when there is a distortion in selection, that is representatives of different classes meet different probability.
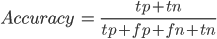
the Accuracy and completeness
the Accuracy (English precision) shows the attitude of truly guessed objects of a class to all objects which we defined as objects of a class. For example, we decided that will buy 115, and from them really bought 37, accuracy means makes 0.33. Completeness (English recall) shows the attitude of truly guessed objects of a class to all representatives of this class. For example, among us guessed really bought 37, and all bought was 43. Our completeness means makes 0.88.

of Fig. 14 — the Table of mistakes or confusion matrix
a F-measure
Also exists a F-measure (English. F1 score) — an average of harmonious accuracy and completeness. Helps to compare models, using one numerical measure.
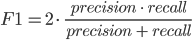
Using all these metrics, we will carry out an assessment of our models.

of Fig. 15 — the Assessment of quality of models on the basis of different statistical metrics
Apparently on the chart, the biggest distortion as models in a completeness metrics (English recall). Neural networks guesses 88% of potential clients, missing only 12%. Old scoring the model missed 36% of percent of potential clients, passing to managers only 64%. Here actually why it is better to entrust Neural networks to select coefficients of the importance of the different answers influencing scoring. After all the car is capable to keep all selection in the memory, to find in it regularities and to build the model possessing good predictive ability.
model
When at us is ready model, we can use it, expecting that accuracy to which to us gave the analysis of its quality. If there is an opportunity to introduce difficult (multilayered) model in the process, it is good but if is not present, it is possible to receive habitual scoring model from single-layer Neural networks. Exactly for this purpose we so in detail examined the device of Neural networks safely to glance it under a cowl.
we Will compare a formula linear scoring models and function of work of one neuron (or single-layer Neural networks):
we See
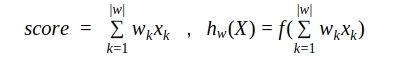 . Means, "having pulled out" values of a matrix of scales from single-layer Neural networks, we can use them as in coefficients scoring models. Only now these coefficients are picked accurately up by algorithm on the basis of a large number of data.
. Means, "having pulled out" values of a matrix of scales from single-layer Neural networks, we can use them as in coefficients scoring models. Only now these coefficients are picked accurately up by algorithm on the basis of a large number of data. Now we will compare results linear scorings on the basis of coefficients before introduction of Neural networks. Let's remember that logistic function of activation gives value (from the point of view of Neural networks — probability of belonging to a class bought) bigger 0.5 at positive value of argument (scorings on the basis of a matrix of scales). We increased values neural scorings by hundred for the purpose of scaling of points and added five hundred as threshold value. At old scorings the threshold through passage was selected manually and made hundred seventy. All these simply linear manipulations which are not influencing in any way model.

of Fig. 16 — Distribution of the bought (red) and not bought (blue) clients within old scoring models
Apparently from distribution, clients are too strongly smeared on all range of values scorings. Completeness (a share predicted by model) makes 64% of all number of the bought clients.

of Fig. 17 — Distribution of the bought (red) and not bought (blue) clients within neural scoring models
From distribution is visible that Neural networks coped with a problem of division of the bought and not bought users it is better than old model. Not bought, in the main weight, received values below threshold, bought — above. Completeness (a share predicted by model) makes 88% of all number of the bought clients.
Result
Solving our problem we wanted to find as much as possible time for those who will buy a tariff for a large sum. Besides, we wished to create such scoring model in which the clients buying the cheapest tariff, would not gather a lowest passing score.
This time for training Neural networks we divided selection into a class bought for a certain sum above, and on a class bought for the smaller sum or not not bought.

of Fig. 18 — Distribution of the bought (red) and not bought (blue) clients within final neural scoring models
At other, almost equal indicators of accuracy, Neural networks could achieve bigger completeness and could capture 87% bought expensive tariff plans. For comparison: old scoring consulted only from 77%. Means, in the future we will be able to cover another 10% of powerful and potential clients. Thus the percent bought expensive tariffs from last scoring is almost identical: 23% and 24% for Neural networks and old model respectively. Thus it is visible that value well correlates scorings with the purchase sum.
of Fig. 19 — Comparison of quality old and new scoring models
So, in this article we:
- Considered all main stages Data Mining.
- were Learned by many useful receptions both by preparation of data, and when training.
- Rather deeply got acquainted with the theory of classical Neural networks.
- were Considered by different statistical approaches to the analysis of quality of model.
- all stages from creation before analysis and introduction Described Neural networks on the example of construction linear scoring models.
- Showed how modern algorithms Machine training can help with the solution of real business challenges.
If you still had questions, wishes or remarks, let's discuss in comments.