
It is known that the last revolution in Cryptography happened in 1976 because of the article "New Directions in Cryptography" of the American scientists Uitfild Diffi (Whitfield Diffie) and Martin Khellman (Martin Hellman). This work was for the subsequent development Cryptography as "Big Bang" — there was a birth the new installed asymmetric Cryptography. Up to this point (in any case in the open press) there was only a symmetric Cryptography. Young and to anybody then not known scientists for the first time offered the scheme in which for development of the general secret subscribers initially did not need to exchange any confidential keys. Besides the pervozdannost this algorithm is interesting to that in spite of the fact that the "difficult" tasks which are cornerstone of it to safety can become outdated, they can be replaced successfully new. Initially it was the problem of discrete logarithming in multiplicative group of a final field (Discrete Logarithm Problem, abbr. — DLP), now in practice are widely used a problem of discrete logarithming in group of points of an elliptic curve (Elliptic Curve of DLP — ECDLP). In the future (not such far) it is supposed to use other "difficult" tasks which will have exponential complexity not only on classical, but also on Quantum computer. They are called post-quantum. One of such tasks is the problem of stay isogeniuses between elliptic curves about which I want to tell in this article.
As article purpose – it is simplest toto explain new mathematical "cursor" for Diffi-Martin Khellman (Diffie-Hellman or in abbreviated form — DH), some attacks are not considered: we assume that the malefactor can read only messages in the channel, but cannot interfere with operation of the channel to intercept messages of subscribers and to send the (i.e. the malefactor not "The person in the middle"). In practice (for example, in by TLS) on open keys of DH the signature can be appended and here already the Person In the middle DH cannot change a key: from the server to the client the open key of DH comes as the certificate, from the client to the server – temporary (ephemeral) the key signed on a constant closed key of of the client. Generally, in severe reality PKI based on trust of both parties to one UTs. But, besides, not to distract the reader from the main thing – mathematics, about PKI I write nothing in this article. And once again: as cases when systems in which the parties exchanged temporary (ephemeral) open keys which the parties in any way did not check were realized and took root (it is visible those who projected them considered itself as too busy persons to study bases Cryptography or at least to address to experts) are known, I ask not to forget that in real life it is necessary. The person In the middle (he is an Intermediary, it is Man-in-the-middle) is not the Yeti and it exists.
Last: classical Diffi-Khellman Alisa and Bob initially are chosen by parameters (domain parameters): multiplicative group of a final field and g — the generator of its subgroup. Terrible in the word the generator is not present anything. It only one of group elements with the following property: if to take it to degree from 1 to number of elements of group, we will receive all group entirely. The subgroup is a subset of group, which in itself – too group (at multiplication of its elements in any combinations, we will receive only elements of this subset).
Primer:F∗p – multiplicative group of a final field.
group Elements:
numberfrom 1 to p — 1, where p – a prime number.
Group operation a*b mod p: we multiply group an and b elements, then we divide a*b into p. a*b remainder of division on p also is result of the operation a*b mod p.
For example, let the module p is equal 11. It is most often designated as F∗11. Consists from 11 – 1 = 10 elements: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
the Number of elements in group is called as order of group (group order). The order of F∗11 is equal 10.<"70>" to
A now we will play with operations a little:
5*6 mod 11 = 8,
1*10 mod 11 = 10.
1 for this group is a neutral element. Neutral — since it "does not interact" with any other elements and the result of operation with it is always equal to the second element of operation. In this case 1*10 mod 11 — are 10.<"72>"
6*2 mod 11 = 1.
For any element of any group exists the return element which "turns" it into the neutral. For this group 6 and 2 – the return for each other.
When group operation is called as multiplication (as in case of F∗p), use such designations for the return to of a an element: a−1 I.e. of a = 1 That else can be told −1∗ about this group? It is commutative (or abeleva):
a∗b mod p = b∗a mod p: from an and b shift the result does not change.
Now about generators: these are such elements, which all degrees which all values of elements of group give. Groups in which there is at least one such element call cyclic. How to understand, what x – the generator? The most primitive method: to construct the table of degrees x:
As about degrees 2?
2*2 mod 11 = 4
4*2 mod 11 = 8
8*2 mod 11 = 5
5*2 mod 11 = 10
10*2 mod 11 = 9
9*2 mod 11 = 7
7*2 mod 11 = 3
3*2 mod 11 = 6
6*2 mod 11 = 1 — we see that the cycle became isolated. Degrees 2 generate all group F∗11.
Total: 2 — the F∗11 generator.
an element Order – the minimum degree in which it should be built to receive the neutral. The order 2 is equal in F∗11 10.
Now we will consider degrees 3:
= 99*3 mod 11 = 5
5*3 mod 11 = 4
4*3 mod 11 = to 1
the Order 3 is equal to
3*3 mod 11 5. It does not "run" all F∗11 values since we see that on the fifth degree there is a cycling: if to continue multiplication, again we will receive 3, 9, 5, 4, 1.
That else can be told about 3?
It too generator. But not for F∗11, and for its subgroup consisting of five elements {3, 9, 5, 4, 1}. it is easy for
to see that this subset of F∗11 - a subgroup: there is a neutral element 1. Isolation: the result of any a*b mod p for these numbers does not go beyond this set, after all the result will be one of a set {3, 9, 5, 4, 1}.
Each element has the return: 3*4 mod 11 = 1, 9*5 mod 11 = 1, 1*1 mod 11 = 1. What else subgroups are in F∗11?
Still there is a group about 2: {1, 10}
Well and certainly trivial subgroups {1} and {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (since formally the group is a subgroup itself)
As it is possible to optimize generator search for F∗11?
Here need to use the base of the theory of groups – Lagrange's theorem: "The order of a subgroup divides a group order".
the Element x or is the group generator, or is the generator of one of its subgroups. Therefore, construction x in degrees of orders of subgroups and comparison of result with 1 can confirm or disprove it.
we Will return to F∗11. Thanks to Lagrange's theorem we absolutely surely can tell that there are nontrivial subgroups only orders 2 and 5 as the order of F∗11 is equal 10.
Thus we could reduce calculations for 2, having built it only in degree 2 and 5!
2∗2 mod 11 = = 22 *22 * 2 mod 11 = 4∗4∗2 mod 11 = 10 ≠1 these calculations is enough Now 4 ≠1
25 mod 11 to prove that 2 – the F∗11
generator Similarly for 4: by
4*4 mod 11 = 5 ≠1 ok, the following step we consider the fifth degree for 4:
45 mod 11 = 42 *42 * 4 mod 11 = 5*5*4 mod 11 = 100 mod 11 = 1-> 4 is not the F∗11 generator How to be if the structure is slightly more difficult? Let's consider F∗19:
Order 18 = 3*3*2. Dividers 18: 2, 3, 6, 9 we Choose a random element, for example 3:
Is built 3 in r1 degree = 18/3 = 6:
36 mod 19 = Is built by 7 ≠1
3 in r2 degree = 18/2 = 9:
39 mod 19 = 18 ≠1
Absolutely not necessarily to build a studied element in degree of all subgroups i.e. 2, 3, 6, 9 since if the element will appear the generator of a subgroup of a subgroup, all the same exponentiation of an order of a subgroup will give 1.
For example if we chose not 3, but 11, would stop on the first shage:
116 mod 19 = 1.
since 11 has an order of 3
116 mod 19 = 113∗2 mod 19 = 12 mod 19
3 in F∗19 generates a subgroup of {1, 7, 11}
Nontrivial subgroups of F∗19: {1, 18}, {1, 7, 11}, {1, 7, 8, 11, 12, 18}, {1, 4, 5, 6, 7, 9, 11, 16, 17}
But we will return to DH. In practice it is a choice of parameters for it is a choice big (~23072, t.e length of 3072 bits) a prime number of p and the generator of of g , an order of of q which (t.e the minimum degree which gives as a result of 1: gq mod p=1) – too a large prime number of (~2256). Basic operation which is carried out in algorithm – exponentiation x on the module: gx mod p.
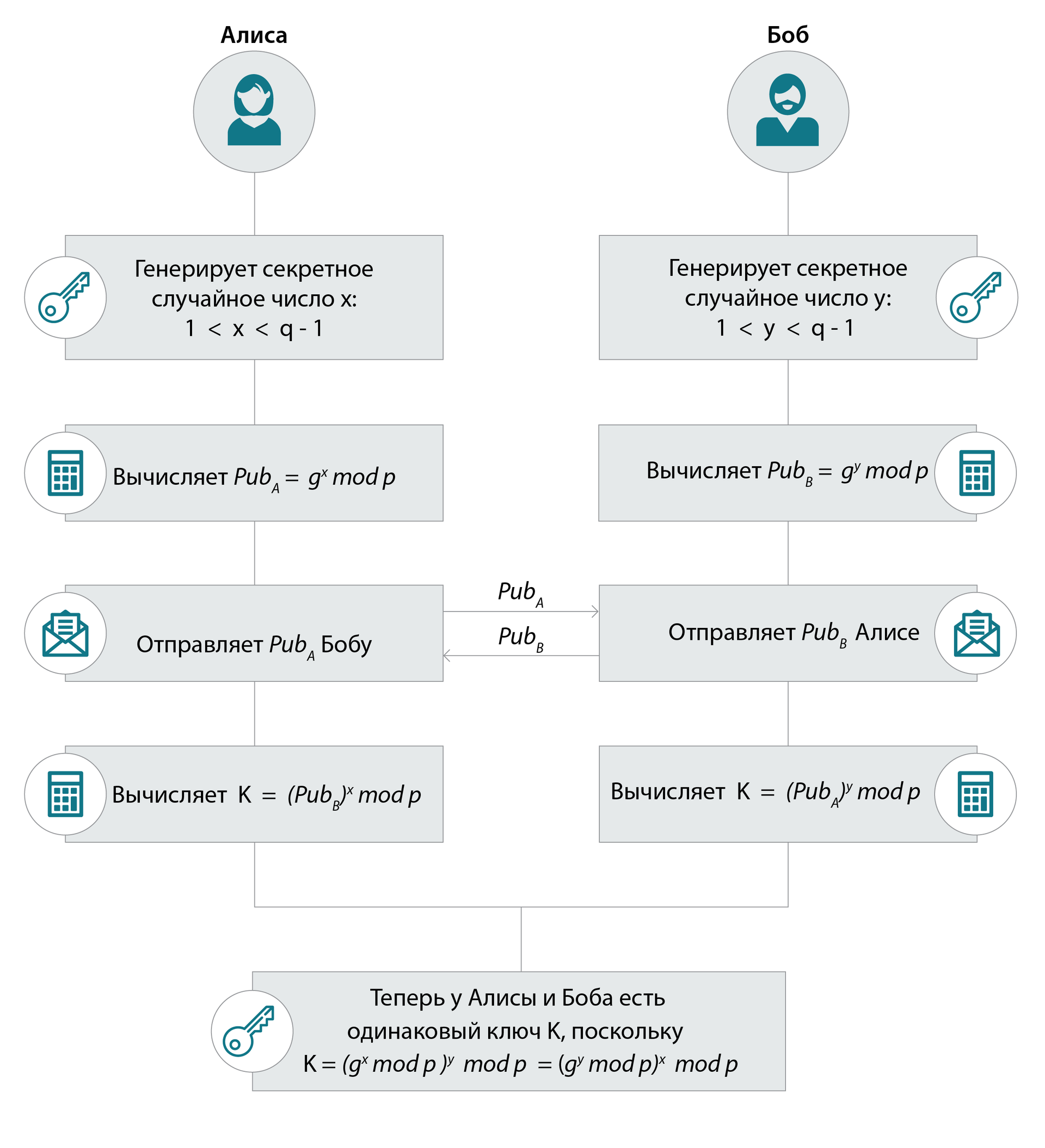
Note: Khellman Alisa and to Bob needs to check keys coming from the outside on accessory to their "working" subgroup of a big simple order of q:
Khellman Alisa checks PubqB mod p = 1? If is not present, interrupts.
Bob Similarly arrives: it checks the key which has come from Khellman Alisa: PubqA mod p = 1?
We now do not consider the opponent who could change open keys on the road, but nevertheless always it is necessary to remember, as in Cryptography cases from the category "at such friends and enemies are not necessary to us" meet: the program on devices Khellman Alisa or Bob may contain various mistakes (in realization of modular arithmetics, or memory can simply be damaged).
If testing underwent normally, Khellman Alisa and Bob consider keys for symmetric algorithms that already with their help to protect a data link (for example to cipher data and to consider MAC (Message Autentication Code) or it is simple to consider MAC).
the Return operation to gx mod p is called as Discrete Logarithm (DL) or on ours Discrete Logarithming: let p, for g and gx be known. It is required to find degree x. It just that is very interesting to the malefactor.
are engaged in the Choice of group certainly not personally Khellman Alisa or Bob, and cryptographers (though, all Alis' some subset and Beans belongs to their set, but we do not consider this special case). Subset of cryptographers who deeply understand a structure of groups and know what of them to use safely are published sometimes by results of the work in the form of concrete numbers of p, g and step-by-step descriptions of algorithms with test vectors. They can be found in a type of the NIST or RFC standards.
Here example of unsafe parameters for DH: the group of a "smooth" order i.e. at which the number of elements can be presented in the form of work of degrees of small prime numbers since in it it is possible to calculate easily a discrete logarithm by means of the Polliga-method Martin Khellman which calculates a discrete logarithm in group subgroups, and then by means of the Chinese theorem of the remains receives a logarithm for the group. As calculations according to the Chinese theorem in itself are rather simple, complexity of all algorithm of Polliga-Martin Khellman can be estimated approximately, as complexity of calculation of DL at the biggest of subgroups of a simple order.
Real: elliptic Diffi-Martin Khellman
B 1985 Neil Koblits (Neal I. Koblitz) and Miller Victor independently from each other invented (Victor Saul Miller) as it is possible to use elliptic curves in Cryptography. Their opening helped to create elliptic options of algorithms of Diffi-Martin Khellman, El-Gamalya, MQV, DSS, GOST P 34.10-94 which initially used multiplicative group of a final field. As a result new algorithms (except for GOST) received EC prefix: ECDH, EC ElGamal, ECMQV, ECDSS. And our Russian GOST P 34.10-94 was transformed to GOST P 34.10-2001 (and then to more reliable 34.10-2012). Why such transition to elliptic curves was necessary? He allowed to carry out faster calculations at the same level of safety.
Khellman Alisa and Bob choose Domain parameters (domain parameters) for elliptic curves.
Of what Domain parameters for elliptic curves consist:
1. To Paula Galois GF(pn). Consists of pn of elements where p —
the characteristic weeding (prime number)
(In practice more often use n = 1. GF ( of p by ) is designated and is called as
as a simple field (prime field). Its elements — all numbers from 0 to p-1)
2. Curve Weierstrass's equation over the field GF(pn) ("Over a field" means that
all coefficients (in this case A and B) and decisions (x and y) – field elements):
y2 = x3 %2BA x %2BB (for p> 3)
where A and B such that 4A3 %2B27B2 ≠ 0, x, y – affine
of the coordinate
of
3. The order of group of points (number of all its elements) Is designated by
as %23E(GF(pn))
Is represented as q*k where q (a large prime number) – a subgroup order, and k – small
the number (not necessarily simple) is called cofactor (factor) of
4. Generator of a subgroup of group of points of a curve (base point): the point of Q having an order of q. (The algorithm of discrete logarithming of Polliga-Martin Khellman is applicable as well to group of points of an elliptic curve, as well as to any other abelevy group therefore the group of points has to have a "rough" order. I.e. equal to work of a large prime number on small number. Unlike classical the option which group always contains p-1 an element, group of elliptic curves can have and a simple order) we Will remind
the basic:
group Elements — is curve points, i.e. couples (x, y) — solutions of the equation of Weierstrass. Group operation is called as addition of points:
(x1, y1) %2B (x2, y2) = (x3, y3)
Plus still is a so-called Point On Infinity (Point At Infinity) or a zero point (but the point on infinity – sounds more beautifully, agree) we Will designate its O. It is analog of unit for multiplicative group of a final field (from classical DH): 1*t mod p = t*1 mod p = t, for curves: (x, y) %2B O = O %2B (x, y) = (x, y). Its fundamental difference from the sister from multiplicative group is that it cannot be presented in the form of any elements of a field i.e. as a usual point (x, y) so that it was possible to carry out with it calculations as with other points on the general formula.
In the first part of article we will consider only the simple field GF (p) therefore all examples and formulas use mod p suffix:
Formula of addition of points (X1, Y1) and (X2, Y2):
X3 = µ2 – X1-X2 mod p
Y3 = µ (X1 — X3) — Y1 mod p
where µ = mod p (Y2-Y1)/(X2-X1), if X1 ≠ X2:
If X1 = X2 and Y1 = Y2 ≠ 0, µ = (3X12 %2BA) / 2Y1 mod p
In a case when X1 = X2 and Y1 = — Y2 mod p, formulas are inapplicable also result – a point on infinity.
of Fraction help to express more beautifully the return element in multiplicative group: for example, (Y2−Y1)/(X2−X1) mod p means (Y2−Y1) *(X2−X1)−1 mod p where (X2−X1)−1 — the return to (X2−X1)
value we Will designate a scalar product of number of n on Q point so: [n] ] * Q.
[n] * Q = Q %2B Q %2B … %2B Q %2B Q
n of times (it is consecutive done n of times addition operation by means of the formulas given above) the Malefactor knows domain parameters: curve and Q point (the subgroup generator) and also result of multiplication of a scalar of n on Q point: [n] ] * Q. That he wants to find: n number (t.e to solve ECDLP problem). In what case it is easy? Captain Obvious says that if Q belongs to a subgroup of the small size, the point [n] * Q will belong to the same subgroup and the malefactor will touch all possible scalars and to multiply them by Q, yet will not receive a point [n] known to it * Q. Therefore Q has to belong to a subgroup of a big simple order.
So, the main group has to contain a subgroup of a big simple order (in other words the order of all group has to be NOT smooth). Captain Obvious again in business also reports: that the group might contain a big subgroup, it is necessary that the group was big. The order of group of points of a curve of E over the field GF(pn) is designated as %23E(GF(pn)). Hasse's theorem gives very useful assessment:
of %23E(GF(pn)) = pn %2B 1 – t, where t – a trace of Frobenius, which t on an absolute value ≤ 2*√pn. I.e. %23E(GF(pn group order)):
pn %2B 1 – √pn ≤ %23E(GF(pn)) ≤ %2B √pn
Now we know pn %2B 1 how the number of elements of a field is connected with number of points: they practically does not differ one after another. Whether it is possible to claim, what for the malefactor it is necessary an order of points of a curve of calculations for receiving a scalar? For "brutforsa" – yes, but after all there is more beautiful method which demands much less efforts. It is a method of Pollard which also we will apply and to DLP (as well as to any other commutative group). It is probabilistic algorithm and number of operations which he demands — about a square root from among elements of group i.e. ~. Thus, if we consider "fighting" cryptographic curves (with q*k, where q a large prime number, and k – small number: in practice 1, 2 or 4) that is convenient to estimate their safety as — number of operations which the malefactor by means of the most advanced method for these curves – Pollard's method has to execute.
Example:
curve NIST P-256 Most often used in the world over a simple field:
group Structure is as follows: an order is equal to a large prime number. T.E of q*k, q – simple and k = 1. Its safety can be estimated as 2128 as today for NIST P-256 of anything better than Pollard's method it is not thought up.
Besides curves with smooth order is also others which allow to solve rather easily ECDLP: supersingular (with t Frobenius's trace such that: t mod p = 0) and abnormal (t = 1). Let's assume that Bob's curve and Khellman Alisa does not get in one of these bad companies and therefore practically to solve ECDLP for it it is impossible.
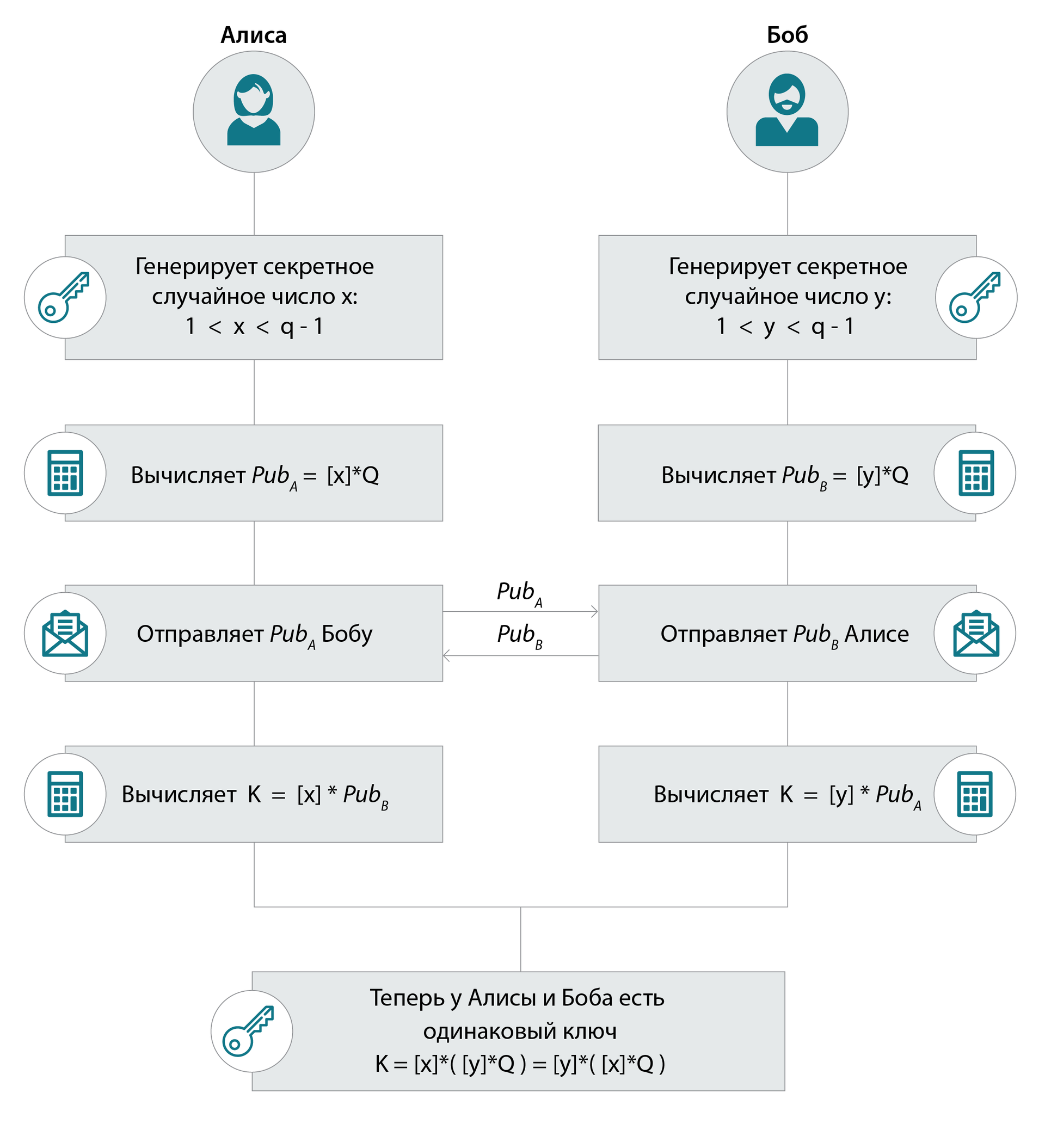
Note: as well as in a case with classical DH, a good form check of all (entering and proceeding) points on belonging to group is considered, but here the situation is a little bit more difficult. At first coordinates are substituted in the equation is a check on entry into group. For check on accessory it is absolutely optional to big subgroup of an order of q to multiply a point by q. It is enough to know orders of small subgroups and to increase a point by them: if as a result we receive a point on infinity, the point in a small subgroup means and has to be interrupted.
Total:
Classical DH: as a result of an exchange of keys at Khellman Alisa and Bob there is an identical element of group: its generator increased by of time:
A now copypaste:
Elliptic DH: as a result of an exchange of keys at Khellman Alisa and Bob there is an identical element of group: its generator — Q point, put time: [x*y] * Q
the Difference in the name of operations for these groups (addition or multiplication) is not important (after all the group only has only one operation). So now more we will try more universally:
as a result of an exchange of keys at Khellman Alisa and Bob appears an identical element of group: its generator over which group operation with it was performed time.
Quantum nightmare and hatred.
Classical and elliptic DH besides mathematical grace unites one unpleasant fact: difficult (for ordinary computers) problems of ECDLP and DLP, being their cornerstone can be easily solved if Quantum computer which are capable to hold in the connected state rather large number kubit (from several hundred to several thousand) are created. krome that, it means the end for RSA cryptosystem: Shor's quantum algorithm allows to decompose large numbers to simple multipliers for polynomial time. Therefore the post-quantum subject is very actual for asymmetric algorithms. For symmetric codes everything is not so awful yet – them will attack quantum algorithm of Grover which has complexity a square root from the power of a set of a key. For example, if you used AES with a length of key of 128 bits to keep the same level of safety the same AES, but with the 256th bit key is necessary (and AES-128 falls to 64 bit levels, i.e. attacking it will be necessary to execute 264 of operations on Quantum computer).
of One of the most perspective complex mathematical challenges steady against Quantum computer are isogeniuses of elliptic curves. About about them I will tell in the following part of article.
Literature:
Shnayer Bruce, Fergyusson Nils "Practical Cryptography" Alfred J
. Menezes, Paul C. van Oorschot and Scott A. Vanstone "Handbook of Applied Cryptography"
Lawrence C. Washington "Elliptic Curves: Number Theory and Cryptography, Second Edition"