Квантовые вычисления и криптология

Развитие вычислительной техники движется по различным направлениям, не ограничиваясь явлениями классической физики, электроники, оптики и теперь уже квантовой механики.
Ознакомление с проблемой квантовой криптологии и смежными, близкими к ней (не только по публикациям), показало, что имеют место определенные недостатки и пробелы в ее описании и представлении. Описывая конкретику того или иного физического явления, объекта, автор игнорирует его окружение даже ближайшее, оказывающее на объект непосредственное воздействие (часто возмущающее влияние). Это не упрек авторам, их право излагать так как они излагают. Это скорее мой мотив включиться в общий поток сознания. Материальная вещественная сторона квантовых явлений так или иначе проявляет себя и неучет ее, может сказаться существенным негативом. Что имеется ввиду? Материальная реализация квантовых компьютеров (КК), регистров, отдельных кубитов — всего того из чего КК сделаны. Обмен пользователей полученными результатами через сети связи и, наконец, защита, целостность и доступность таких результатов от нарушителя — тоже проблемы.

Квантовая криптология и смежные вопросы

Новое направление физики — квантовая информация — возникло на стыке квантовой механики, оптики, теории информации и программирования, дискретной математики, лазерной физики, спектроскопии и включает в себя вопросы квантовых систем связи, квантовых вычислений, квантовых компьютеров, квантовой телепортации и квантовой криптологии, проблемы декогеренции и спектроскопии одиночных молекул и примесных центров.
Даже не касаясь криптологии, квантовая физика опирается и использует для описания своих понятий и явлений такое большое количество классических физических явлений, по которым в школьной физике (да пожалуй и в ВУЗовской) прошлись «галопом» или вообще мимо, что почти каждое понятие (вроде бы знакомое) требует пояснений в силу новых открытий и достижений последних лет, что в рамках статьи сделать практически невозможно. Но этот отбор материала — проблема автора, а не читателя.
В теории криптологии (криптография + криптографический анализ) также можно выделить несколько периодов (этапов) развития. Древняя симметричная криптология (одноключевая, обе стороны канала связи используют один ключ); асимметричная или двухключевая криптология (шифруется сообщение открытым ключом, а расшифровывается другим – закрытым). Наконец,
следующий этап развития криптологии покрывает настоящее время и начался с осознания возможности построения квантового компьютера (КК) и квантовой криптологии.
Специалисты классической криптологии поняли и признали, что такой компьютер – мощнейший инструмент криптографического анализа шифров, который в считанные секунды сможет взламывать классический шифр любой стойкости. Но они увидели и другую (положительную) сторону открывающихся возможностей – возможность построение квантовой криптографии с практически не взламываемыми шифрами.
Идея квантовой криптографии зародилась практически одновременно с идеей использовать квантовые объекты для вычислений, т. е. с идеей создания квантового компьютера и системы связи, использующей квантовые каналы наряду с традиционными.

Квантовый канал системы связи и его элементы

Уже сегодня мы живем в мире квантовых сетей, которые растягиваются на тысячи километров и выходят в космос. На мировом рынке коммерческих систем квантовой коммуникации доминируют три компании: китайские Qasky и QuantumCTek, а также швейцарская ID Quantique (с 2001). Они поставляют практически весь спектр решений и компонентов: начиная с источников и детекторов одиночных фотонов, квантовых генераторов случайных чисел до интегрированных устройств. В России такая сеть связала два офиса “Газпромбанка” в 2016 г, расположенных друг от друга на расстоянии около 30 километров. В этом же году КНР запустила спутник QUESS — Quantum Experiments at Space Scale, «Квантовые эксперименты космических масштабов»), который обеспечил квантовое распределение ключей на расстоянии свыше 7600 км между обсерваториями в Пекине и в Вене.

Схема квантового канала связи

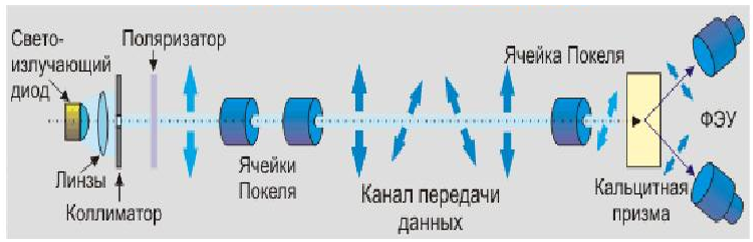
Рисунок 1. Схема квантового канала и протокола квантового распределения ключа
Идея и реализация квантовой криптографии иллюстрируется рисунком 1. На изображении слева — передающая сообщения сторона, справа – приемная. Важными необходимыми элементами системы являются ФЭУ, выполняющие роль фотодетекторов, ячейки Поккельса (Покеля), кальцитная призма (Волластона), поляризатор. Конечно, без остальных элементов: светоизлучающего диода на основе квантовой точки (лазера), линз, коллиматора, оптоволокна и потока фотонов систему не поcтроить, но эти элементы хорошо известны, используются давно и во многих системах c совершенно с другим назначением. Квантовый канал с ИСЗ реализуется без оптоволокна.
Для отдельных элементов схемы сделаем пояснения.
Фото́н — элементарная частица, квант электромагнитного излучения в виде поперечных электромагнитных волн и переносчик электромагнитного взаимодействия. Это безмассовая частица, способная существовать в вакууме, только двигаясь со скоростью света. Электрический заряд фотона также равен нулю. Фотон может находиться только в двух спиновых состояниях с проекцией спина на направление движения (спиральностью) ±1. Мюон —квант мюонного поля. Фотон — квант электромагнитного поля. В физике фотоны обозначаются буквой γ.
Светоизлучающий диод. В 2001 году Эндрю Шилдс и его коллеги из TREL и Кембриджского университета создали диод, способный испускать единичные фотоны. Это дало возможность передавать поляризованные фотоны на большие расстояния. В ходе экспериментальной демонстрации удалось передать зашифрованные данные со скоростью 75 Кбит/с — при том, что более половины фотонов терялось.
Ячейка Поккельса (иногда называют ячейкой Покеля) и представляет собой кристалл, помещенный между двумя скрещенными николями. Николи не пропускают свет в отсутствие электрического поля, а при наложении поля пропускание появляется. Внешнее поле (силовые линии) может быть перпендикулярно распространению света (поперечный модулятор) или параллельно (продольный модулятор).
Эффект Поккельса (эффект назван в честь Ф. Поккельса, изучившего это явление в 1893 году) – явление изменения показателя лучепреломления света в кристаллах (оптических средах) при воздействии постоянного или переменного электрического поля. Он отличается от эффекта Керра тем, что линеен по полю, в то время как эффект Керра квадратичен. Эффект Поккельса наблюдается только в кристаллах, не обладающих центром симметрии: в силу линейности при изменении направления поля эффект должен менять знак, что невозможно в центрально-симметричных телах.
Эффект хорошо заметен в кристаллах ниобата лития или арсенида галлия.
Эффект Поккельса, как и эффект Керра, практически безынерционен (быстродействие порядка 10^-10 с). Благодаря этому он находит активное применение в создании оптических модуляторов. Практическая реализация эффекта осуществляется ячейками Поккельса.
Квантовая точка (КТ) — миниатюрный кусочек полупроводникового материала диаметром 15 нм и толщиной 5 нанометров (нм), который может при подаче на него тока захватывать лишь по одной паре электронов и дырок.
Существует два главных метода создания квантовых точек:

При помощи коллоидного синтеза можно получать нанокристаллы, покрытые слоем адсорбированных поверхностно-активных молекул. Таким образом, они растворимы в органических растворителях, после модификации — также в полярных растворителях.
Выращивают в основном соединения из элементов III (Ga, Al, In) и V (As, P, Sb) групп таблицы Менделеева — группы обозначаются AIII BV (или А₃, В₅). На основе таких КТ созданы полупроводниковые лазеры и СВЧ-транзисторы.
Особый интерес представляют флуоресцирующие квантовые точки, получаемые методом коллоидного синтеза, например, квантовые точки на основе халькогенидов кадмия в зависимости от своего размера флуоресцируют разными цветами. Явление на практике знакомо даже детям, так как широко применяется в сотовых телефонах.
Физико-химические свойства квантовых точек
Широкий спектр поглощения, что позволяет возбуждать нанокристаллы разных цветов одним источником излучения. Узкий и симметричный пик флуоресценции (без «хвоста» в красной области, как у органических красителей, полуширина пика флуоресценции 25—40 нм), что обеспечивает чистый цвет: точки размером 2 нм — голубой, 3 нм — зеленый, 6 нм — красный.
Высокая яркость флуоресценции (квантовый выход >50 %). Высокая фотостабильность.
Функционирование квантового канала (системы) связи. Отдельные фотоны светоизлучающего диода фокусируются линзой и проходят через коллиматор, после чего попадают в устройство поляризации, где поляризуются к требуемому (одному из 4-х (|, –, \, /)) виду с использованием ключа шифра. Фотоны перемещаются, сохраняя поляризацию, по каналу системы связи и на приемной стороне вновь проходят через ячейку Поккельса, после которой попадают на кальцитную призму (Волластона), разделяющую единый поток фотонов на два, направляя каждый на свой ФЭУ. Последние, используя ключ шифра, считывают информацию, преобразуя ее в сообщение для получателя.

Предпосылки квантовых вычислений

Идея квантовых вычислений в 1980 г. высказана Ю. И. Маниным [1] и в 1982 г. в статье Р. Фейнмана [2]. Становление квантовой механики, в рамках которой получены результаты, необъяснимые классической механикой явилось толчком для развития не только физики, но и ряда других научных направлений, в числе которых квантовые связь, вычисления, криптология.
Для удобства описания квантовых понятий и явлений при вычислениях и манипулировании с переменными по аналогии с цифровым двоичным битом (binary digits = bit) введено понятие квантового бита (quantum bit) – кубит.
Называют также несколько физических моделей квантовых вычислений: ионные ловушки, фотонные кубиты, топологические кубиты и т. п.
Определение. Кубит – наименьший элемент для хранения информации в квантовом компьютере. В соответствии с законами квантовой механики кубит может одновременно находиться в двух собственных состояниях, обозначаемых |0⟩ и |1⟩.
Кубитом может быть любая двухуровневая квантовая система, например, квантовая частица со спином ±½ в постоянном магнитном поле (электрон, ядро, фотон). При этом состояние кубита может быть задано суперпозицией А|0⟩+В|1⟩, где А и В – комплексные числа, удовлетворяющие условию |A|² + |B|² = 1, т.е. частица переходит в одно из собственных состояний с вероятностями перехода |A|² в 0 и |B|² в 1. Техника вычислений с кубитами достаточно подробно дана ( здесь)
Амплитуды вероятностей описываются формулами: А = cos(½θ); B = -e^iφ sin⁡(½θ).
Конструкция кубита. КК может быть создан при использовании нанометровой кремниевой планарной технологии интегральных схем. При этом должны быть выполнены требования изоляции кубитов от любых степеней свободы, ведущих к декогерентности. Если рассматривать кубиты, как спины на доноре в полупроводнике, то ядерные спины в матрице представляют собой большой резервуар, с которым донорные спины могут взаимодействовать.
Спины в матрице должны быть в состоянии I = 0. Это важное требование исключает все полупроводники видов AIII BV для синтеза матрицы, так как только единственно для кремния существует стабильный изотоп ²⁸Si со спином I= 0. Другое требование — глубокое охлаждение, температура должна быть настолько низкой, чтобы исключалась ионизация донора. Важным требованием в случае рассмотрения двух и более кубитов является требование перекрытия областей квантовых волновых функций Шрёдингера.
Донором для Si (кремний) со спином I = ½ является единственный атом ³¹Р (фосфор). Для системы ²⁸Si: ³¹Р при Т=1,5К и низкой концентрации ³¹Р время релаксации электронного спина около ≈1000 секунд, а время релаксации ядерного спина ³¹Р превышает 10 часов. Квантовые вычисления возможны для ядерных спинов при локализации на положительно заряженном доноре в матрице полупроводника. Температура их должна быть достаточно низкой (3-5 милликельвинов), при которой исключается ионизация донора.
Состояние фотона нельзя прочесть (измерить) дважды. Попытка «перехвата» сообщения будет замечена. При выявлении (измерении) текущего состояния кубита {|0⟩ или |1⟩} состояния должны быть физически различимы и оцениваются вероятностями. Такие вероятности косвенно служат для оценивания исходного (до измерения) состояния кубита. Кубиты можно рассматривать как единичные векторы в двухмерном комплексном векторном пространстве с ортогональным зафиксированным базисом {|0⟩} и {|1⟩}. Квантовая теория поля рассматривает частицы как колебания (кванты) полей. Фотон — квант электромагнитного поля. Мюон — мюонного.
Суперпозиция состояний – это, что-то вроде списка всех возможных состояний квантового объекта (допустим фотона). До того, как его измеряли. Это не совсем волна и не совсем частица, а что-то другое, имеющее похожие свойства — «волница, вейвлет».
При одновременном рассмотрении нескольких кубитов (регистра кубитов) изменение состояния одного из кубитов приводит к изменению состояний других. Они изменяются согласованно с первым.
Такая связь называется запутанностью состояний, а множество кубитов интерпретируется как заполненный квантовый регистр квантового компьютера. Этот регистр может находиться в различных состояниях и реализовывать обмен и тонкие физические зависимости между кубитами.
Требования к КК
Сформулированы также требования и общие условия создания твердотельного КК:

• обеспечение «долговечности» работоспособности квантовой системы (до перехода в декогерированное состояние);
• обеспечение реализации нанометровых (100…1000Å) расстояний между кубитами, изоляция кубитов от любых степеней свободы, которые могут приводить к декогерентности;
• наличие квантового регистра, в котором размещается ансамбль кубитов (масштабирование-допускать увеличение разрядности);
• наличие низких температур, обеспечивающих перевод всех кубитов в основное (начальное) состояние для предотвращения неконтролируемых переходов с нижних уровней, сопровождаемых переворотом спина;
• постоянное магнитное поле, снимающее вырождение по спину, ∆Ее = µВgеB, ∆ЕN = =µNgNB, где В – магнитное поле, µВ, µN – магнетон Бора и ядерный магнетон соответственно; gN, gе – ядерный и электронный g – фактор;
• возможность управления состояниям кубитов путем воздействия импульсами высокочастотного электромагнитного излучения (ЭМИ) различной длительности и фазы для поворота спина на заданный угол;
• возможность индивидуализации кубитов (измерения состояний отдельных кубитов), путем подачи напряжения на специальные операционные затворы одноэлектронных транзисторов;
• возможность выполнения одно- и двух- и n-кубитных логических операций с использованием затвора связи между кубитами;
• располагать «универсальным» набором вентилей, например, набор, включающий вентиль Адамара, вентиль фазового сдвига, вентиль CNOT и вентиль π⁄8. С их помощью можно выполнить любое квантовое вычисление на произвольном наборе кубитов.

Требования к обработке квантовой информации и ее передаче (обмене ею):
а) Система должна обладать способностью надежно преобразовывать данные, хранящиеся в виде стационарных (вычислительных) кубитов в сетевые (передающиеся) кубиты (например, фотоны) и обратно.
б) Система должна обладать способностью корректно передавать сетевые кубиты между конечными точками.

Создание КК и его элементов

Квантовые компьютеры развиваются стремительными темпами. Создаются КК на нескольких различающихся принципах: ЯМР — ядерный магнитный резонанс, ЭСР — электронный спиновый резонанс, ядерный спин в кремнии. Частицей порождающей кубиты может быть электрон, ядро, фотон, способные к изменениям спинового состояния.
Квантовым компьютером (КК) называется твердотельное (полупроводниковое) устройство, использующее квантовые физические явления и свойства электронных (ядерных) спинов для выполнения вычислений при решении задач
Существует множество платформ, на основе которых можно построить универсальный квантовый компьютер. Однако, у каждого подхода есть свои недостатки. Например, сверхпроводящие кубиты имеют небольшие времена когерентности по сравнению с другими реализациями, а из холодных атомов трудно построить большой квантовый компьютер.
Квантовые точки — перспективная реализация кубитов, но и они имеют множество проблем. Одна из них — качественное измерение кубитов, которое не разрушает квантовое состояние системы. В данном контексте кубитами считаются одиночные электроны в квантовых точках, а состояния 0 и 1 описываются электронным спином.

Квантовый компьютер на ядерных спинах в кремнии

Разработчикам КК было от чего отталкиваться в своей деятельности. Нанометровая кремниевая планарная технология интегральных схем работает, функциональные требования перечислены, ограничения и условия в основном определены. Система Si:³¹Р исчерпывающе изучена около 60 лет назад в экспериментах по электрон-ядерному двойному резонансу.

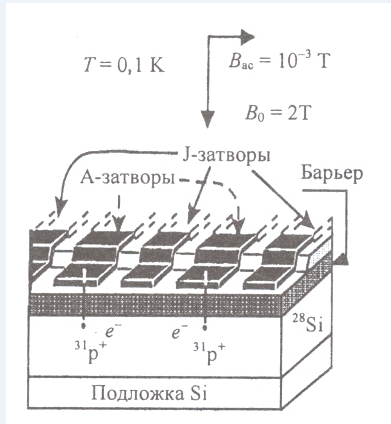
Рисунок А — Два кубита в одномерном регистре (два донора ³¹Р со связанными электронами, внедренными в ²⁸Si )
При низкой концентрации ³¹Р и при Т =1,5 К время релаксации электронного спина — порядка 1000с, а время релаксации ядерного спина ³¹Р превышает 10 часов. При снижении температуры до 0,1 К, исключающей ионизацию донора волновая функция электрона концентрируется у ядра донора, что приводит к сверхтонкому взаимодействию между спинами ядра и электрона.Пластина кремния помещается в постоянное магнитное поле Во≥ 2Т.
Два кубита в одномерном регистре содержат два ³¹Р донора со связанными электронами с внедренными в ²⁸Si. Они отделены от управляющих металлических затворов на поверхности слоем SiO₂. А- электроды управляют (задают) резонансной частотой ядерно-спинового кубита; J — затворы управляют взаимодействием электронов соседних ядерных спинов.

Квантовый компьютер на электронном спиновом резонансе

При использовании ЭСР чистота изотопа матрицы кремния некритична. По ряду показателей ЭСР предпочтительнее ядерного спина, магнитное поле в 2 Тл (Тесла) обеспечивает частоту ЭСР равную 56 ГГц, и из-за высокой зеемановской энергии электронные спины позволяют работать вплоть до частот гигагерцового диапазона. Ядерные спины — только до 75 кГц. При Т= 1 К спины электронов (в отличие от ядерных) полностью поляризованы. Вместо кремния используются гетероструктуры Si/Ge, что обеспечивает возможность управлять эффективной массой донорного электрона.Ненужными оказываются J-затворы ячеек.Для измерений (прочитывания результатов) можно использовать не одноэлектронные транзисторы, а обычные полевые при низких температурах.

Рисунок В — Иллюстрация метода детектирования спинового состояния электрона
Человек непосредственно не может наблюдать состояния кубитов и квантовых регистров. При приложении напряжения к А затворам оба электрона с антипараллельными (синглетное состояние) спинами (левый и правый) оказываются связанными с одним и тем же донором (D ^— состояние).Они могут выполнять переходы в новые состояния, что приводит к появлению электрического тока, который измеряется с помощью емкостного устройства (одноэлектронного транзистора). Это обеспечивает определение спинового состояния электрона и ядра донора ³¹Р. При этом реализуется принцип Паули.

Рисунок С — Схема обменного взаимодействия между двумя кубитами (двухкубитная операция)
При увеличении напряжения на затворе уменьшается энергия связи и увеличивается боровский радиус водородоподобных доноров. В ху-плоскости электроны могут быть электростатически притянуты к одному из барьеров, образованных В-слоями состава Si_0,23 Ge_0,77. Кулоновский потенциал уменьшается V=-q/√(r² + d²), где r² =x² +y² — квадрат горизонтального расстояния от донора, а d- вертикальное расстояние от барьера до донора.
При этом снижается энергия кулоновской связи электронов и повышается перекрытие их волновых функций, разрешая проводить двухкубитные операции.
Конструкция ЭСР кубита
Будем рассматривать строение ячейки регистра КК для двух кубитов. Материальная ячейка ЭСР создается методом выращивания на кремниевой основе (кристалле) твердого раствора Si/Ge, поверх которого последовательно наращиваются еще 5 рабочих слоев.

Рисунок Д — Строение ячейки ЭСР для двух кубитов
Слева (а)- энергетический профиль гетероструктуры Ge _{1 — х}Si_х; справа (б) — поперечный разрез двухкубитной ячейки. ПТ — полевые транзисторы; <111> — ориентация подложки.
Основные слои Т (tuning) «настроечный» и D2-донорный без разрывов зон проводимости, где выполняются квантовые вычисления (между атомами 2000 Å). Толщина и состав слоев определяются энергетической диаграммой (слева) и требованиями воздействия управляющих затворов (сверху слоев). Слои Т и D2 заключены между барьерными (их толщина 200Å) слоями, запрещающими электронам двигаться вертикально, отличаются составом и имеют разный g- фактор: g(T) = 1,563; g(D2)= 1,995 Электроны слоя D2 играют роль кубитов. Разрывы зон проводимости равные 20 мэВ реализуют запрет и сохранение кубитных донорных электронов как носителей, так и квантовой информации.

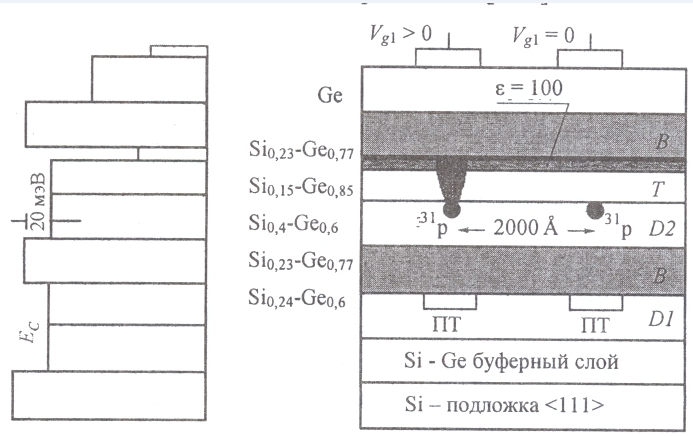
Рисунок Е — Строение ячейки ЭСР для двух кубитов. Сохранены обозначения предшествующего рисунка
Рассмотрим влияние ориентации подложки кристаллического кремния. Ориентация подложки, обозначаемая символом [001] (кристаллографическая теория) дает некоторые преимущества. быстрее изменяется энергия зоны проводимости для этого направления, можно выбирать твердые составы с меньшими напряжениями при высоте барьера около 50 мэВ, что более 2-х кратного увеличения, по сравнению с ориентацией [111].
Соответственно барьерные слои при сохранении той же вероятности туннелирования могут быть тоньше (миниатюризация), а допустимые напряжения значительно выше.Использование слоя с параметрами, приводящими к увеличению боровского радиуса и, следовательно, к увеличению возможного расстояния между кубитами, привело к эпитаксиальному нанесению активного слоя с большей диэлектрической проницаемостью. С ростом расстояний существенно уменьшается обменная частота между кубитами.
Для КК на основе ЯМР на атомах фосфора в кремнии нашли решение достаточно сложной проблемы при создании кубитов — точного расположения донорных атомов (до 100Å)

Рисунок F — Схема процесса построения регистра из ячеек ЯМР кубитов
Схема размещения отдельных атомов фосфора в кремнии стала реализуемой благодаря достижениям нанотехнологии. Очищенная в условиях сверхвысокого вакуума поверхность пластины кремния (Si [001]2×1) пассивируется монослоем водорода. Затем по специальной программе с помощью зонда сканирующего туннельного микроскопа десорбируются в заданных местах отдельные атомы водорода. После этого в камеру вводятся пары фосфина при давлении 10 ^-8 мм рт. ст. Адсорбированные молекулы фосфина затем при температуре 500°С диссоциируют, оставляя атомы фосфора, связанные с кремнием, в местах адсорбции. После этого производится низкотемпературное заращивание кремнием полученной структуры.
Появляется возможность создать компьютер, способный к параллельным вычислениям на уровне всего вычислительного устройства.
Перечислим факторы и факты, увеличившие интерес к КК, и стимулы их практической разработки.
Для квантовых вычислителей созданы алгоритмы, решения трудных задач:

• поиск элементов (перебором) в неструктурированной базе данных 1996 (L.K. Grover );
• моделирование эволюции квантовых систем, например, ядерных реакций;
• задача факторизации больших чисел (ЗФБЧ) 1994 (P.W. Shor );
• вычисление дискретного логарифма (ДЛОГ) в конечном поле, на эллиптической кривой;
• и др.

Разработана процедура управления квантовыми состояниями (коррекции квантовых ошибок ).
Выполнен эксперимент, реализующий квантовые вычисления, для алгоритма Гровера и других на жидкостных ядерных магнитно-резонансных КК.
На основе твердотельных элементов созданы варианты конструкций КК:

• на основе квантовых точек (D.Loss, G.Burkard, L. Fedichkin, K.Valiev);
• на основе сверхпроводящих переходов Джозефсона (D.E. Averin);
• на ядерных спинах донорных атомов фосфора ³¹Р в изотопически чистом ²⁸Si (B.E.Kane).
• на электронных спинах тех же атомов фосфора в эпитаксиальных гетероструктурах
• Ge1-x Six (D. DiVincenzo).

Ниже приводятся формулы оценивания состояний кубита и их вероятностей.
Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:1) в волновой механике — волновой функцией; 2) в матричной механике — вектором.
Квантовые компьютеры обещают изменить многое в нашем мире. По своей природе они хорошо приспособлены к вычислениям, которые необходимы для обращения односторонних функций. Для симметричной криптографии это не так уж плохо. Алгоритм Гровера показывает, что квантовый компьютер ускоряет атаки настолько, что эффективная длина ключа уменьшается вдвое. То есть 256-битный ключ так же сложен для квантового компьютера, как 128-битный ключ для обычного компьютера: оба они безопасны в обозримом будущем.
Для криптографии с открытым ключом ситуация более тяжелая. Алгоритм Шора легко ломает все популярные алгоритмы с открытым ключом, основанные как на факторизации, так и на дискретном логарифмировании. Удвоение длины ключа увеличивает сложность взлома в восемь раз. Этого недостаточно для устойчивого функционирования (механизм коррекции ошибок на квантовом компьютере легко может стать непреодолимой проблемой для них).
Шифрование с открытым ключом (используемое главным образом для обмена ключами)
Ключевое слово здесь «обмен ключами» или, как говорят обычно, согласование ключей. А само шифрование (AES, «Кузнечик», «Магма» и т.п.) выполняется на симметричных ключах (естественно с периодической сменой ключей, всякие keymeching-b, может даже выработкой для каждого пакета). Речь идет только о ключе шифрования.
В квантовой физике (механике) действует ряд принципов, отсутствующих в традиционной классической физике.
Принцип неопределенности Гейзенберга, невозможно одновременно получить координаты и импульс частицы, невозможно измерить один параметр фотона, не исказив другой.
Принцип исключения Паули утверждает, что два электрона (или два любых других фермиона) не могут иметь одинаковое квантово-механическое состояние в одном атоме или одной молекуле.
Другими словами, ни одна пара электронов в атоме не может иметь одинаковые электронные квантовые числа. Принцип запрещает клонирование (копирование) кубитов.
Клонирование — это такая операция над парой или более кубитов, в результате которой создается состояние, являющееся тензорным произведением идентичных состояний подсистем.
Теорема о запрете клонирования (копирования) — утверждение квантовой теории о невозможности создания идеальной копии произвольного неизвестного квантового состояния частицы. Теорема была сформулирована Вуттерсом, Зуреком и Диэксом в 1982 году и имела огромное значение в области квантовых вычислений, квантовой теории информации и смежных областях.
Состояние одной квантовой системы может быть сцепленным с состоянием другой системы. Например, создать сцепленное состояние двух кубитов можно с помощью однокубитного преобразования Адамара и аппаратно — двухкубитного квантового вентиля C-NOT. Результатом такой операции не будет клонирование, поскольку результирующее состояние нельзя описать на языке состояний подсистем (состояние является нефакторизуемым).

Сложным является вопрос о том, как интерпретировать получаемый результат.
Преимущества и недостатки квантовой связи и КК перед классическим.
Положительные стороны использования квантовых систем.

• КК оперирует при вычислениях не числами, а квантовыми состояниями;
• в традиционной (классической) физике индивидуальные состояния частиц объединяются при помощи обычного скалярного умножения векторов; при этом возможное число состояний из n частиц образует векторное пространство размерностью 2ⁿ;
• в квантовой системе состояние кубита выражается линейной комбинацией (суперпозицией) базисных состояний |0⟩ и |1⟩ или {|0⟩} и {|1⟩}. Поэтому квантовые состояния объединяются посредством умножения тензоров. При этом результирующее пространство состояний для n квантовых частиц (пространства n векторов) получается с размерностью оцениваемой величиной 2ⁿ. Одна частица – два {|0⟩ и |1⟩} состояния; две частицы – четыре состояния {00, 01, 10, 11} и т. д. Линейный рост числа частиц приводит к экспоненциальному росту числа состояний;
• на регистре из m кубитов одновременно (параллельно) можно выполнять вычисления над 2^m числами. Явление называется квантовым параллелизмом.
• из этого следует подобное возрастание скорости вычислений.

Тензорное произведение состояний – причина EРR paradox и в какой-то мере объяснение его.

Тензорное произведение

Рассмотрим случай 2-х кубитов.

Случай 2-х кубитов. Возможны 4 варианта их совместного состояния
Эти 4 вектора в столбцах таблицы являются базисными в пространстве двух кубитов. Формально это описывается так. Если имеются пространства Н1 и Н2 с размерностями d1 и d2 и ортонормированными базисами {ei} и {fj}, то можно определить пространство с базисом {

}, где i принимает значения от 1 до d1, а j – от 1 до d2.
Если ввести на новом пространстве скалярное произведение по закону

и продолжить его на остальные векторы, то в результате получится гильбертово пространство, которое называется тензорным произведением Н1 и Н2 и обозначается

. Очевидно, что его размерность равна d1d2.
Тензорное произведение операторов

и

– это оператор

в пространстве

, действующий по закону (

). Возникает вопрос о том всякое ли состояние в пространстве

можно задать как тензорное произведение состояний, принадлежащих частичным пространствам Н1 и Н2?
Ответ на этот вопрос отрицателен, и классическим контрпримером является состояние в пространстве двух кубитов

, называемое ЭПР по первым буквам фамилий первооткрывателей (Эйнштейн, Подольский, Розен):

.
Легко видеть, что это состояние нельзя представить в виде тензорного произведения одночастичных состояний:

.

Квантовая криптология

Квантовая криптография (ККГ) — метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить конфиденциальность информации, ККГ ориентирована на физические явления, рассматривая случаи, когда информация переносится с помощью объектов квантовой механики.
Квантовый криптоанализ (ККА). Широкое распространение и развитие квантовой криптографии вызвало появление противовеса — квантового криптоанализа, который в ряде случаев обладает, согласно теории, преимуществами перед обычным. RSA и другие теоретико-числовые шифры и методы криптографии основанные на проблемах факторизации больших чисел, нахождении дискретного логарифма утратят стойкость с появлением квантового ККА.
По законам физики состояние кванта света (фотона) нельзя прочесть дважды: после первого воздействия на фотон его состояние изменится и повторная попытка даст другой результат. Попытка «перехватить» информацию будет замечена. Поэтому квантовая криптография сегодня считается наиболее перспективным направлением шифрования.
Для решения этих проблем был разработан, в частности, квантовый алгоритм Шора (1994), позволяющий найти за конечное и приемлемое время все простые множители больших чисел или решить задачу логарифмирования, и, как следствие, взломать шифры RSA и ECC. Поэтому создание достаточно крупной квантовой криптоаналитической системы является плохой новостью для RSA и некоторых других асимметричных систем. Необходимо только создание квантового компьютера, способного исполнить необходимый алгоритм.
По состоянию на 2012 год наиболее продвинутые квантовые компьютеры смогли разложить на множители числа 15 (в 150 тыс. попыток верный ответ был получен в половине случаев, в соответствии с алгоритмом Шора) и 21.
Защита информации (сообщений) от несанкционированного доступа и от модификации с использованием квантовых объектов была высказана еще в 1970 году Стивеном Визнером. Беннет С.Н. и Ж. Брассард спустя 10 лет предложили использовать эти объекты для передачи ключей шифрования в форме протоколов квантового распределения ключа – ВВ84 и позднее в 1991 и 1992 году усовершенствованный протокол.
Квантовая криптография наряду с преимуществами и выгодами характеризуется и определенными ограничениями, и негативными сторонами. Как в любой коммуникационной системе в системе связи, использующей квантовую криптографию, имеются узлы с пользовательским приемо-передающим оборудованием, каналы связи, источники энергии и пр.
К отмечаемым негативным аспектам квантовой связи обычно относят следующие.
На обеих сторонах (передающей и приемной) канала квантовой системы связи должна быть установлена сложная аппаратура:

• несовершенство источников одиночных фотонов (малая скорость генерации);
• система управления поляризацией фотонов слабо защищена от помех;
• несовершенство приемников одиночных фотонов, чувствительные детекторы срабатывают кроме фотонов и на другие частицы;
• затухание светового сигнала в среде, что не гарантирует достижение фотоном получателя сообщения; ограничивается дальность передачи;
• при удаленности абонентов более 100 км (интенсивность падает в 100 раз) требуются репитеры, но для квантовой криптографии этому препятствует теорема о запрете клонирования (невозможно создать идеальную копию фотона, а если удастся, то этим может воспользоваться и нарушитель);
• фотоны чувствительны к высоким температуре и вибрациям;
• высокая стоимость оборудования (один сервер $81000).

Для измерения угла поляризации фотонов необходимо точно знать, как ориентировано оборудование на обоих концах канала. Эти условия ограничивают распространение квантовой криптографии на мобильные устройства.
Со временем был найден приемлемый вариант. Сложное оборудование можно устанавливать лишь одному пользователю, на одном конце канала. Другой пользователь принимает сигнал и только модифицирует состояние фотонов, внося в измененные состояния свою информацию. Измененные фотоны отправляет обратно. Такая аппаратура уже способна разместиться в карманном устройстве.
Что касается установления ориентации оборудования, то предложено выполнять измерения в случайных направлениях, а их список публиковать открыто. При легитимной работе и расшифровании использовать только совпадающие у абонентов направления. Метод получил название «квантового распределения ключей независимого от системы отсчета».

Квантовое распределение ключей

Квантовое распределение ключей (QKD) – метод передачи ключа, который использует квантовые явления для гарантии безопасной связи. Этот метод позволяет двум сторонам, соединенным по открытому каналу связи оптоволоконных или свободных сетей для передачи потока фотонов, создать общий случайный ключ, который известен только им, и использовать его для шифрования и расшифрования сообщений.
Основной целью известных протоколов квантового распределения ключей (QKD) является согласование случайных передаваемых последовательностей частиц (фотонов).
В 1935 году Эйнштейн с группой единомышленников, пытаясь оспорить копенгагенскую интерпретацию квантовой механики, сформулировал парадокс, названный позднее парадоксом Эйнштейна-Подольского-Розена (EРR paradox тензорными методами описываются не все состояния кубитов).
Среди возможных QKD известны ранние ВВ84, В92(Беннетa), В91(Экерта, другое название ЕРR), позднее CW (непрерывные переменные), швейцарский протокол СОW(Coherent One Way-когерентное одностороннее шифрование), Lo05(создан Ло Х.-К. Ма К. и Ченом К. 2005), SARG, Decoy State, DPS(differential Phase Shift), с реперным состоянием, фазово-временной.
Алгоритм Чарльза Беннета (англ. Charles H. Bennett). Ниже рассматриваются подробно некоторые из перечисленного списка протоколы.

Квантовый протокол ВВ84

Пример 1. Реализация квантового распределения ключа шифра (протокол ВВ84), в котором используются ортогональные состояния квантовых объектов. Получатель сообщения воздействует на объекты (фотоны), выбирая случайным образом тип измерения: он изменяет либо прямолинейную поляризацию фотона (|, –), либо диагональную (\, /)
РЕАЛИЗАЦИЯ КВАНТОВОГО ПРОТОКОЛА ВВ84

Протоколы Lo05 и Е91. Этот протокол был разработан Артуром Экертом в 1991 году. Так же он имеет название EPR (Einstein-Podolsky-Rosen) так как он основан на парадоксе Эйнштейна-Подольского-Розена. Lo05 — квантовый криптографический протокол распределения ключей, созданный ученными Ло Х.-К. Ма К. и Ченом К. Квантовое распределение ключей (QKD) позволяет двум пользователям, отправитель и получатель, общаться в абсолютной безопасности в присутствии перехватчика, нарушителя.
В 1991 году Беннет предложил для регистрации изменений в переданных с помощью квантовых преобразований данных использовать следующий алгоритм:

Для того чтобы определить, остались или нет необнаруженные ошибки, получатель и отправитель повторяют псевдослучайные проверки, а именно: получатель и отправитель открыто объявляют о случайном перемешивании позиций половины бит в их строках; получатель и отправитель открыто сравнивают четности (если строки отличаются, четности должны не совпадать с вероятностью 1/2); если имеет место отличие, получатель и отправитель, использует двоичный поиск и удаление неверных битов.
Если отличий нет, после m итераций получатель и отправитель получают идентичные строки с вероятностью ошибки 2 ^{— m}.
Квантовый протокол B92 — один из первых протоколов квантового распределения ключа, который был предложен в 1992г. Ч. Беннетом. Отсюда и название B92, под которым этот протокол известен в наше время. Протокол B92 основан на принципе неопределённости в отличие от таких протоколов, как E91. Носителями информации являются 2-х уровневые системы, называемые кубитами. Важной особенностью протокола является использование двух неортогональных квантовых состояний.

Пример 2. Реализация квантового распределения ключа шифра (протокол В92), в котором используются ортогональные и не ортогональные квантовые состояния (поляризации фотонов).

1. В случае ЭПР-реализации, отправитель случайно выбирает базис для измерения состояния одного фотона из ЭПР-коррелированной пары либо линейный, либо круговой.
2. Во втором шаге действия отправителя зависят от версии протокола.
а) при ЭПР-реализации, выбирает случайную последовательность базисов для измерения поляризаций фотонов;
б) Отправитель выбирает случайную последовательность поляризованных фотонов и отправляет их получателю.
3.Получатель измеряет поляризации пришедших фотонов, используя последовательность случайных базисов.
4. Результаты измерений получателя (не идеальность источника, канала связи и детектора приводят к потере фотонов).
5. Получатель сообщает отправителю базис измерения поляризации каждого полученного фотона.
6. Отправитель сообщает получателю, какие базисы получателем выбраны верно.
7. Отправитель и получатель сохраняют данные о фотонах, измеренных в правильных поляризациях, а все остальные отбрасывают.
8. Оставшиеся данные интерпретируют в соответствии с кодовой таблицей:
9. Отправитель и получатель проверяют их ключи на соответствие по чётности выбранного подмножества бит. Если хотя бы один бит отличается, то такая проверка показывает существование нарушителя, прослушивающего канал.
10. Стороны отбрасывают один из битов выбранного подмножества.
В результате коммуникации по протоколу B92 отправитель и получатель получают общий секретный ключ 0101101 и выявляют отсутствие нарушителя с вероятностью ½.

Квантовый протокол СОW

Пример 3. Реализация квантового распределения ключа шифра (протокол СОW), в котором используются когерентное одностороннее шифрование.
Отправитель посылает ”0” с вероятностью (1 − f)/2, ”1” с вероятностью (1 − f)/2 и контрольные состояния (decoy) с вероятностью f.
Получатель объявляет для каких битов последовательности он провел измерения во временной линии и когда загорался детектор DM2, возвращает последовательность отправителю.
Отправитель выполняет (Просеивание ключа) – сообщает получателю какие биты ему нужно исключить из его сырого ключа, так как они обусловлены детектированием контрольных состояний.
Отправитель. Анализируя срабатывания в DM2, оценивает нарушения когерентности через видности V1−0 и Vd и вычисляет информацию нарушителя.
Выполняется коррекция ошибок. Усиление секретности просеянного ключа
Любопытный факт «отмены коллапса» волновой функции приводится Коротковым и Джорданом.
На него обратили внимание и провели эксперимент, проверяющий и якобы подтверждающий теорию. Но по-видимому, одного подтверждения маловато и об использовании факта никто не опубликовал пока каких-либо идей или приложений. Не упомянуть об этом я просто не мог.
Отмена коллапса опытом (2008) группы Надава Каца, подтверждающим правильность теории Короткова -Джордана (2006) уход от коллапса путем многократных возвратов состояния кубита.
Вообще, любая квантовая система находится в суперпозиции всех своих возможных состояний до тех пор, пока не произойдёт измерение и она примет одно из возможных состояний. После измерения система примет конкретное состояние (коллапсирует).
И вот, в 2006 году Коротков и Джордан публикуют статью с заголовком «Uncollapsing the wave function by undoing quantum measurements», что на русский можно примерно перевести как «Отмена коллапса волновой функции посредством отмены квантового измерения». или arXiv: 0708.0365v1 [ Quant-Ph:

Криптоаналитические уязвимости, атаки, их классификация

Специалистами полагается, что квантовое распределение ключей не является неуязвимым для взлома, а вполне доступно нарушителю. Другое дело, что действия нарушителя могут быть обнаружены, а ключ при этом не востребован и заменен на другой. Конкретные реализации таких систем позволяют проводить успешную атаку и похищать сгенерированный ключ.
Возможен достаточно обширный перечень атак.
Атаки на оборудование квантовой системы:

• использование светоделителя;
• использование мощного импульса (ослепление лавинных фотодетекторов);
• использование спектра источников фотонов, если они различаются;
• использование нарушителем ГПСЧ аналогичного как у отправителя.

Атаки на состояние квантов (фотонов):

• использование когерентности;
• когерентные атаки учитывают тактику ретрансляции;
• некогерентные атаки: перехватчик-ретранслятор; использование клонирования фотонов;
• – атаки комбинированные:
  – взаимодействие с отдельными кубитами;
  – измерения их массивов.

Три примера реализованных атак (по публикациям в сети)

Атака светоделителем на СОW

Предполагается, что реcурсы нарушителя неограничены. Атаки на протоколы распределения ключа: общая схему приготовления и измерения квантовых состояний, процедуру получения результатов измерений квантовых состояний ключа на стороне отправителя и получателя. Атаки на техническую реализацию квантово-криптографических систем (квантовый хакинг).

• Затухание ⇒ µB = 10−δl/10µ;
• Светоделитель + идеальный канал связи;
• µ max E = µ − µB = (1 − 10−δl/10)µ.

В февральском выпуске журнала «Квантовая электроника» (в числе учредителей — ведущие физические институты РАН) описан способ — как прочитать сообщение, передаваемое по квантовой сети связи, реализованной по швейцарской технологии, и при этом остаться незамеченным. Как написано в статье, «основная идея атаки состоит в индивидуальном измерении части перехваченных состояний и пересылке остальной их части в неизмененном виде. Авторами рассчитаны оптимальные значения параметров атаки для произвольной длины канала связи».
Российская разработка имеет больший защитный потенциал для создания многопользовательских сетей за счет особого способа передачи нескольких каналов по одной линии. Это позволяет существенно увеличить скорость или пропускную способность квантового канала, считает разработчик.
Другой пример PNS-атака (Photon number splitting attack) [1], проведенная физиками из Австралии и Японии, которые впервые провели квантовое неразрушающее измерение кубита, который состоял из одного электрона в квантовой точке. Ученые показали, что надежность такого измерения составляет более 99,6 процентов. Статья опубликована в Nature Communications.
Ученые из Австралии и Японии под руководством профессора Сейго Таруча (Seigo Tarucha) из научного центра RIKEN предложили измерять кубит в квантовой точке с помощью другого электрона, запутанного с кубитом. Такая реализация позволяет долго сохранять состояние рабочего кубита, что необходимо, например, для реализации кодов коррекции ошибок.
Для проверки неразрушающего считывания физики поместили два электрона в квантовые точки из Si/SiGe — один из электронов использовался в качестве рабочего кубита, а другой в качестве анциллы для измерения. Связь кубитов ученые контролировали магнитным полем, которое создавал микромагнит на чипе.

Схема физической реализации двух кубитов, представляющих два электрона, которые ученые поместили в квантовые точки. J. Yoneda, et al. — Nature Communications 11, 1144 (2020)
Литература:
Д.А.Кронберг, Ю.И.Ожигов, А.Ю.Чернявский. Квантовая криптография. — 5-е изд. — МАКС Пресс, 2011. — С. 94-100. — 111 с. Архивная копия от 30 ноября 2016
Bennett C. H., Brassard G. Quantum Cryptography: Public Key Distribution and Coin Tossing // Proceedings of International Conference on Computers, Systems & Signal Processing, Dec. 9-12, 1984, Bangalore, India.— IEEE, 1984. — P. 175
Bennett, C. H. and Brassard, G., Conf. on Computers, Systems and Signal Processing, Bangalore, India, 175-179 (1984).
Bennett C.H. Quantum Cryptography using any Two Nonortogonal States // Phys. Rev. Lett. 1992. Vol. 68, 3121.
Ekert A. K., Hutter B., Palma G. M., Peres A.Eavesdropping on quantum-cryptographical systems // Physical Review A. — 1994. — Vol. 2, № 50. — P. 1047-1056
Einstein A., Podolsky B., Rosen N. Can quantummechanical description of physical reality be considered complete? // Phys. Rev. A — 1935. — Vol. 47, 777.
Shor P.W. Scheme for reducing decoherence in quantum computer memory // Phys. Rev. A 1995. Vol. 52, 2493.
Shor P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer // SIAM J.Sci.Statist.Comput. 1997. Vol. 26, 1484.
Shor P.W., Preskill J. Simple proof of security of the BB84 quantum key distribution protocol // Phys. Rev. Lett. 2000. Vol. 85, 44